目次(まとめ)
◾️ 適合度を検定するためのカイ2乗統計量を算出する
◾️ カイ2乗分布のパーセント点をあらわす表をつかって、おおよそのP値を見積もる
◾️ 参考文献
◾️ 関連記事
こんにちは、みっちゃんです。
今回の記事では、2012年に行われた統計検定1級の応用数理(現:統計応用)の共通問題(問2)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
この問題では、サッカーワールドカップで記録されたゴールの数を取り上げています。
| ゴール数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 計 |
| 度数(観測値) | 35 | 35 | 18 | 5 | 2 | 0 | 0 | 1 | 96 |
適合度を検定するためのカイ2乗統計量を算出する
ここでは、以下のような帰無仮説を考えます。
帰無仮説:観測されたゴール数の分布はポアソン分布にしたがう
ポアソン分布については、こちらの記事をご参照ください。
そこで、この帰無仮説が棄却できるかどうかを判断できるようなP値を求めていきます。
仮に、ポアソン分布にしたがうとすると、ゴール数に対する期待値は以下のように得られます。
$$(期待値)= \frac{\lambda^x}{x!} {\rm exp}(-\lambda)\qquad(x = 0, 1, 2, ...)$$
| ゴール数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 計 |
| 度数(観測値) | 35 | 35 | 18 | 5 | 2 | 0 | 0 | 1 | 96 |
| 期待値 | 33.527 | 35.270 | 18.552 | 6.506 | 1.711 | 0.360 | 0.063 | 0.009 | 96 |
"観測値" が "期待値" に合っているか(適合しているか)どうか、つまり、"観測値" がポアソン分布にしたがっているかどうか、を検定するために、以下のようなカイ2乗統計量を算出します。
$$(適合度のカイ2乗統計量)= \sum \frac{(O-E)^2}{E}$$
ここで、"E" は期待値、"O" は観測値を示しています。
それぞれのゴール数について、カイ2乗統計量を計算すると、約0.774になります。
カイ2乗分布のパーセント点をあらわす表をつかって、おおよそのP値を見積もる
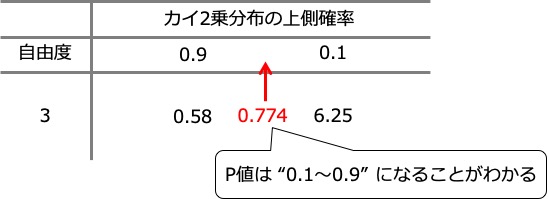
カイ2乗統計量が "0.774" になることがわかりましたが、これをP値に変換する必要があります。
ただし、帰無仮説を棄却できるかどうかを考えるような検定であれば、正確にP値を求める必要はありません。
おおよそのP値を見積もるためには、カイ2乗分布のパーセント点をあらわす表を用います。
この表は、行が「自由度」、列が「カイ2乗分布の上側確率」に相当していて、両方の値が得られれば、「カイ2乗値」を求めることができます。
ここで自由度は、\((カテゴリー数)-2\)です。
カテゴリー数は、ゴール数の種類に相当するので、表からは、8種類あることがわかります。
ただし、ゴール数が多くなると観測値が得られない特徴があるので、ここではゴール数が少ない方から5種類のカテゴリーに注目します。
したがって、自由度は \(3 (=5-2)\) となります。
いま、「自由度」と「カイ2乗値」がわかったので、「カイ2乗分布の上側確率」を見積もることができますが、0.1より大きい値になることは明らかであり、検定が有意にならないことがわかります。
したがって、帰無仮説を棄却することができず、「観測されたゴール数の分布はポアソン分布にしたがう」と判断できることになります。

