目次(まとめ)
◾️ ポアソン分布の確率関数、確率母関数、積率母関数、特性関数
◾️ 確率母関数を使って、平均と分散を算出する
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、大量に観測されたデータの中で、珍しく発生する現象について、その数の分布を表す「ポアソン分布」について解説します。
例えば、「ある交差点を通過する車の中で、交通事故を起こす車の数」「ある工場で生産された製品の中で、不良品の数」「ある都市に住む人の中で、肺がんで亡くなる人の数」など、珍しい現象の確率分布です。
ポアソン分布の確率関数、確率母関数、積率母関数、特性関数
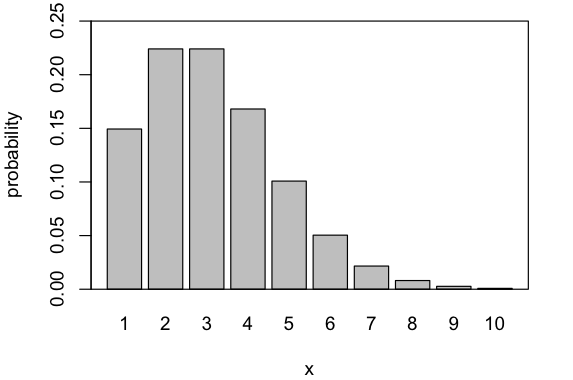
ポアソン分布は、上の図で示すような離散分布であり、強度と呼ばれる1つのパラメータ \(\lambda\) を使って表現されます。
例えば、\(X = 1\) が示すのは「ある工場で生産された製品の中で、不良品が1個」だった確率です。不良品の数は、1個2個・・というように離散値をとるため、離散分布で表現されることになります。
また、離散分布なので、確率密度関数ではなく、確率関数が定義されます。
確率関数
$$P(X = k | \lambda) = \frac{\lambda^k}{k!} {\rm exp} \{- \lambda\} \qquad (k = 0, 1, 2, ...)$$
ちなみに、上の図で示しているポアソン分布の確率関数は、以下のようにRで実行することで得られます(\(\lambda = 3\))。
> x <- 1:10
> barplot(dpois(x, 3), ylim = c(0, 0.25), names = c(1:10), xlab = "x", ylab = "probability")
> box()ポアソン分布の平均や分散は、強度パラメータに一致するため、平均\(\lambda\)、分散\(\lambda\)になります。
平均や分散は、以下の確率母関数や積率母関数、特性関数を用いて取得することもできます(詳細は以下、もしくは、こちらの記事をご覧ください)。
確率母関数
$$G_X(s) = {\rm exp} \{(s - 1) \lambda\}$$
積率母関数
$$M_X(t) = {\rm exp} \{(e^t - 1) \lambda\}$$
特性関数
$$\varphi_X(t) = {\rm exp} \{(e^{it} - 1) \lambda\}$$
確率母関数を使って、平均と分散を算出する
ここでは、ポアソン分布の確率母関数を使って、ポアソン分布の平均と分散を算出する手順を示します。
まず、確率母関数 \(G_X(s)\) は、以下のように与えられます。
$$G_X(s) = {\rm exp} \{(s - 1) \lambda\}$$
確率母関数の定義より、\(G_X(s) = E[s^X]\) という関係があるので、確率母関数を1回微分して取得できる \(G_X^{(1)}(s)\) は \(E[Xs^{X-1}]\) になります。
$$G_X^{(1)}(s) = E[Xs^{X-1}] = \lambda {\rm exp} \{(s - 1) \lambda\}$$
\(s = 1\) とすると、
$$G_X^{(1)}(1) = E[X] = \lambda$$
となり、平均が \(\lambda\) となります。
同様に、確率母関数を2回微分して取得できる \(G_X^{(2)}(s)\) は \(E[X(X-1)s^{X-2}]\) になります。
$$G_X^{(2)}(s) = E[X(X-1)s^{X-2}] = \lambda^2 {\rm exp} \{(s - 1) \lambda\}$$
\(s = 1\) とすると、
$$G_X^{(2)}(1) = E[X(X-1)] = E[X^2] - E[X] = \lambda^2$$
となります。分散が \(E[X^2] - (E[X])^2\) と定義されるので、\(\lambda^2 + \lambda - \lambda^2\) となり \(\lambda\) となります。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

