目次(まとめ)
◾️ Rでは、さまざまな自作関数を定義して描くことができる
◾️ 細かい四角形をつかって、指定した箇所を塗りつぶす
こんにちは、みっちゃんです。
今回の記事では、プログラミング言語であるRを使って、さまざまな関数を図示して、指定した場所を塗りつぶす方法を解説します。
以下のような図を作図することができるようになることを目指します。
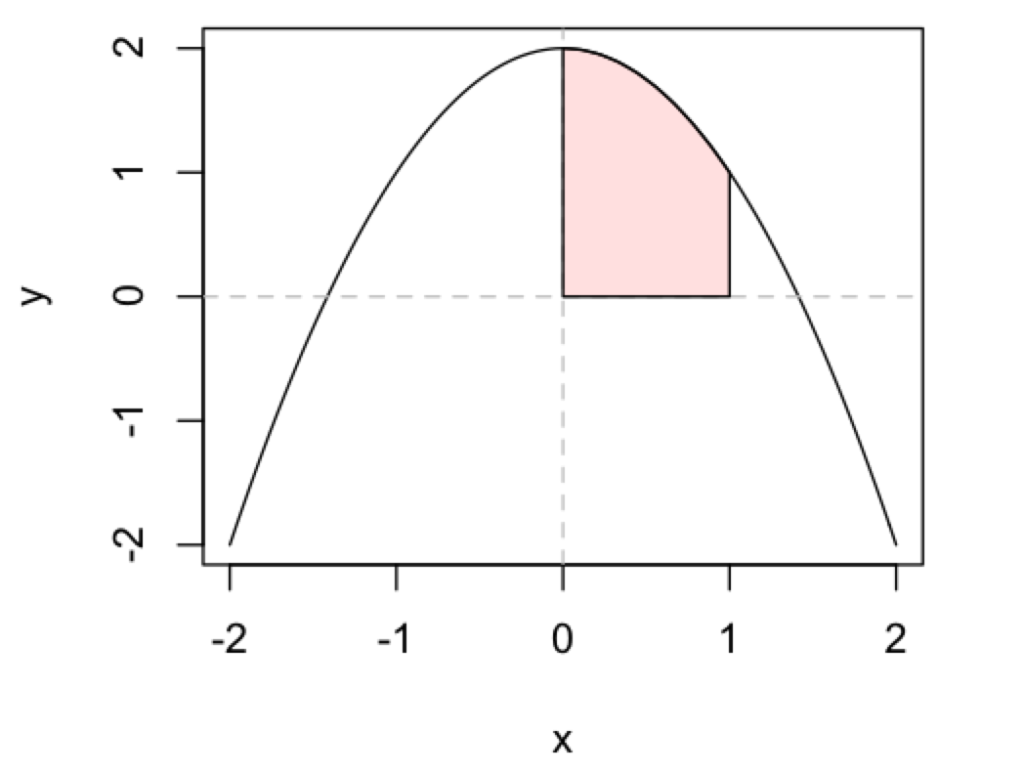
Rでは、さまざまな自作関数を定義して描くことができる
今回の記事では、プログラミング言語であるRを使って解説します。
Rは、MacOSのターミナル(こちらの記事をご参照ください)や、RStudio(こちらの記事をご参照ください)で開くことができます。
ここでは、以下のように、ターミナル上でRを開いて解説していきます。
$ R -q例えば、「\(y = -x^2 + 2\)」という関数を図示したい場合には、以下のように実行することができます。
> curve(-x^2 + 2, -2, 2, xlab = "x", ylab = "y")"curve" というRの関数の中に、図示したい関数、\(x\) の下限、\(x\) の上限、\(x\)ラベルの名前、\(y\)ラベルの名前、を与えています。
これを打ち込むだけで、以下のように描くことができます。
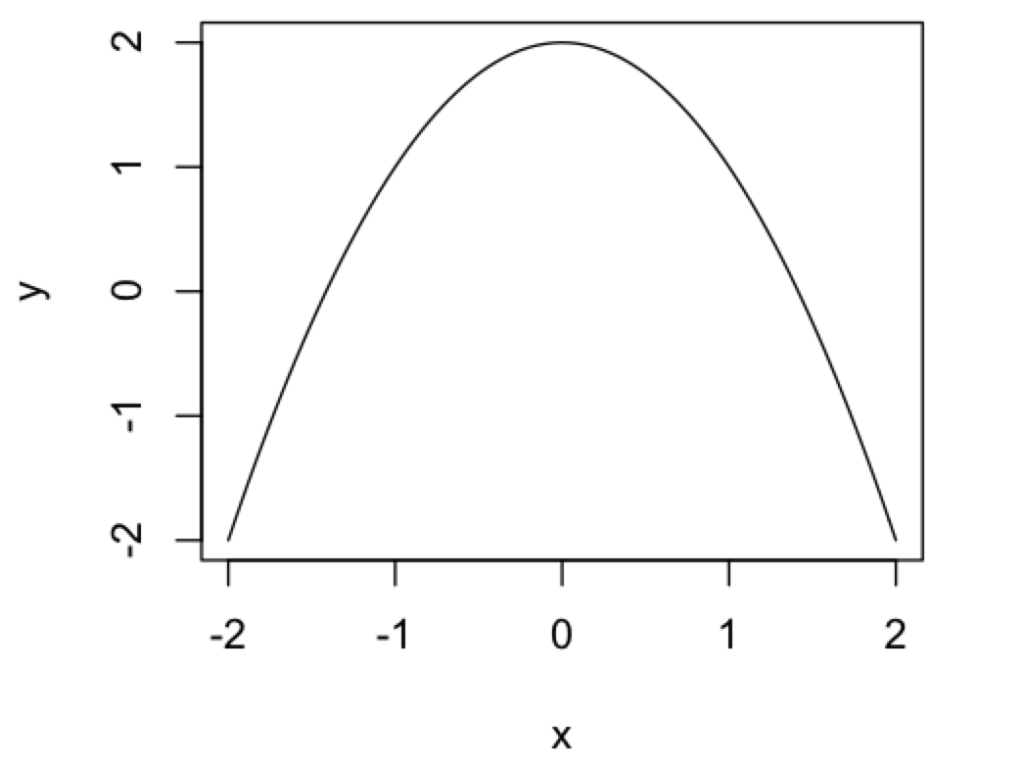
また、いまプロット範囲いっぱいに関数が描かれていますが、以下のように、\(x\) 軸の範囲 "xlim" や \(y\) 軸の範囲 "ylim" を追加して実行すれば、プロット範囲を調整することができます。
> curve(-x^2 + 2, -2, 2, xlab = "x", ylab = "y", xlim = c(-3, 3), ylim = c(-5, 5))また、\(x\) 軸に並行な直線は、以下のように描くことができます。
> abline(h = 0.0)ここで、"h = 0.0" と指定することで、\(y = 0\) の直線が描かれます。
また、 \(y\) 軸に並行な直線は、以下のように描くことができます。
> abline(v = 0.0)ここで、"v = 0.0" と指定することで、\(x = 0\) の直線が描かれます。
さらに、例えば、点線で灰色の線にしたい場合には、点線にするオプション "lty = 2"、灰色にするオプション "col = "gray"" を追加して、以下のように実行します。
> abline(h = 0.0, col = "gray", lty=2)
> abline(v = 0.0, col = "gray", lty=2)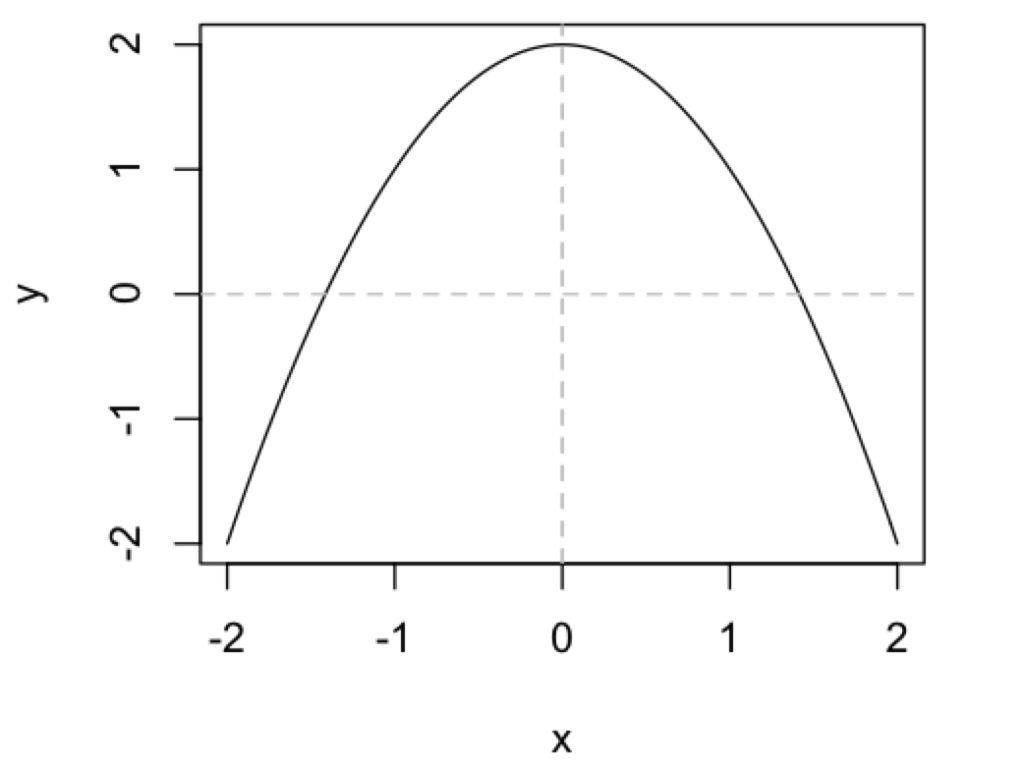
細かい四角形をつかって、指定した箇所を塗りつぶす
ここでは「上に凸の二次関数と \(x ~ (0 \leq x \leq 1)\) 軸に囲まれた領域」を塗りつぶすことを考えます。
これを実現するためには、\((x, y)\) 座標の \((0, 0), (0, 2), (1, 0), (1, 1)\) で囲まれる領域を塗りつぶせばいいということになります。
したがって、以下のように記述することができます。
#1 > x <- c(0, 1)
#2 > y <- as.numeric(lapply(x, function(x) {return (-x^2 + 2)}))
#3 > x2 <- c(x, rev(x))
#4 > y2 <- c(rep(0,2), rev(y))
#5 > polygon(x2, y2, col="#FF000020")1行目では、\(x\) の座標を指定しています。同じ操作は "x <- seq(0, 1, length=2)" としても実行できます。
2行目では、指定した \(x\) の座標に対する \(y\) の座標を取得するために、lapply関数を使っています。"function(x) {return (-x^2 + 2)}" の "-x^2 + 2" の箇所に関数を指定するだけです。
3行目では、領域を指定する4角の \(x\) 座標を "x2" として指定しています。rev関数は、xに入っている数値の順番を逆にするので、"x2" には "0, 1, 1, 0" が保存されることになります。
4行目では、領域を指定する4角の \(y\) 座標を "y2" として指定しています。rep関数は、"rep(0,2)" とすることで "0" を2回繰り返すので、"y2" には "0, 0, 1, 2" が保存されることになります。
3行目と4行目で、原点から時計回りに4角の座標を指定しています。
5行目で、polygon関数に4角の座標を与えることで、四角形を図示します。"col" で色を指定していますが、赤のカラーコードである "#FF0000" に20%透明度を指定しています。
これを実行すると、以下のようになります。
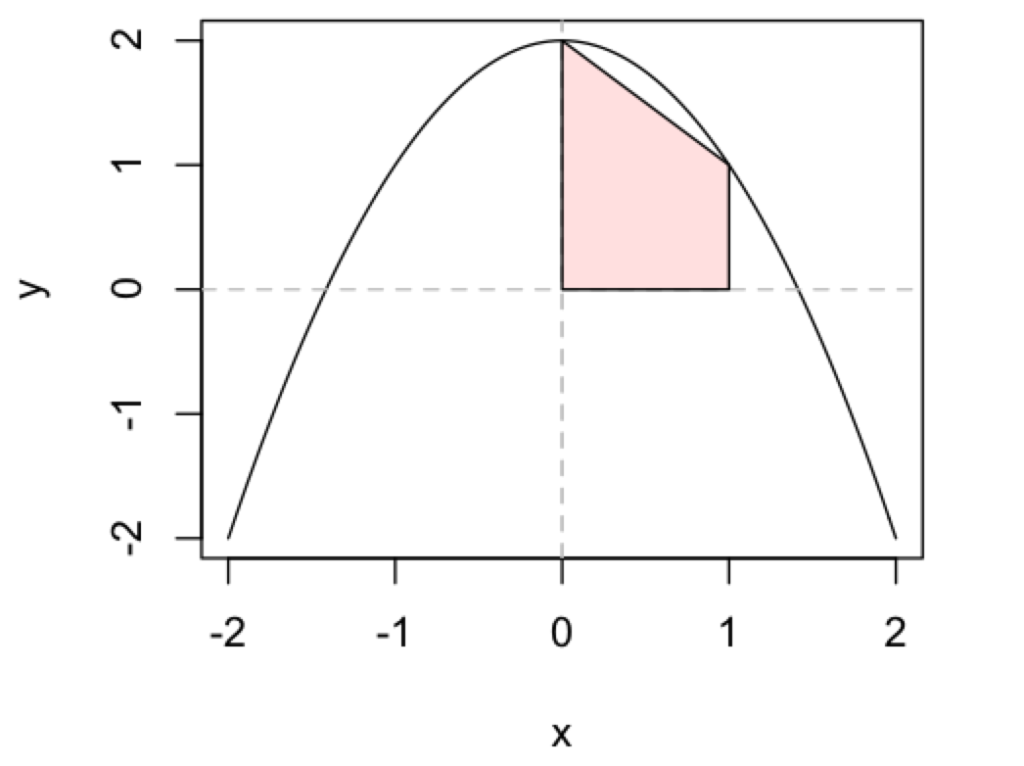
当然、曲線の下の領域は、四角形で表すことができないので、塗りつぶされない場所が存在することになります。
そこで、以下のように、四角形を多くすることで対処します。
> curve(-x^2 + 2, -2, 2, xlab = "x", ylab = "y")
> abline(v = 0.0, col = "gray", lty=2)
> abline(h = 0.0, col = "gray", lty=2)
> x <- seq(0, 1, length=100)
> y <- as.numeric(lapply(x, function(x) {return (-x^2 + 2)}))
> x2 <- c(x, rev(x))
> y2 <- c(rep(0,100), rev(y))
> polygon(x2, y2, col="#FF000020")

