目次(まとめ)
◾️ ガンマ分布の確率密度関数、積率母関数、特性関数
◾️ 形状母数と尺度母数が確率分布に及ぼす効果
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、正の値を示す確率変数の分布の代表格である「ガンマ分布」について解説します。
ガンマ分布の確率密度関数、積率母関数、特性関数
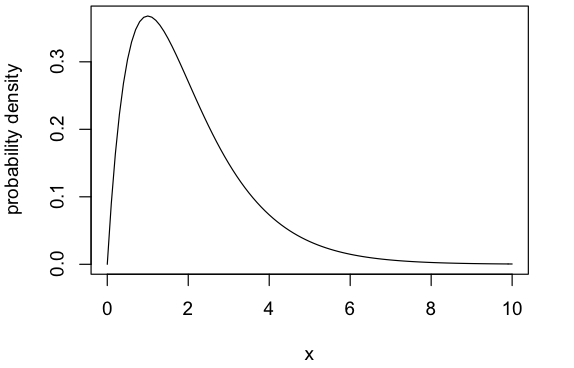
正規分布は、平均\(\mu\)と分散\(\sigma^2\)という2つのパラメータからなる確率密度関数 \(f_X(x | \mu, \sigma^2)\) によって表現されていました(詳細はこちらの記事をご覧ください)。
同様に、ガンマ分布は、形状母数\(\alpha\)と尺度母数\(\beta\)という2つのパラメータをつかって表現されます。
ちなみに、上の図で示しているガンマ分布の確率密度関数は、以下のようにRで実行することで得られます(\(\alpha = 2, \beta = 1\))。
> curve(dgamma(x, 2, 1), xlab = "x", ylab = "probability density", xlim = c(0, 10))ガンマ分布の確率密度関数は、以下のように得られます。
確率密度関数
$$f_X(x | \alpha, \beta) = \frac{1}{\Gamma (\alpha)} \frac{1}{\beta} (\frac{x}{\beta})^{\alpha -1} {\rm exp}\{- \frac{x}{\beta}\}$$
ここで、\(\Gamma (\alpha)\)はガンマ関数と呼ばれる関数で、以下のように定義されます。
$$\Gamma (\alpha) = \int_{0}^{\infty} y^{\alpha -1}{\rm exp}\{-y\}dy$$
また、平均や分散は、以下の積率母関数や特性関数を用いて取得することができます(詳細はこちらの記事をご覧ください)が、平均\(\alpha \beta\)、分散\(\alpha \beta^2\)になることを確認できます。
積率母関数
$$M_X(t) = (1 - \beta t)^{- \alpha}$$
特性関数
$$\varphi_X(t) = (1 - \beta it)^{- \alpha}$$
形状母数と尺度母数が確率分布に及ぼす効果
ガンマ分布には、形状母数といわれる \(\alpha\) と、尺度母数といわれる \(\beta\) という2つのパラメータがあります。
まず、尺度母数 \(\beta = 1\) に固定して、形状母数 \(\alpha\) を変化させてみます。
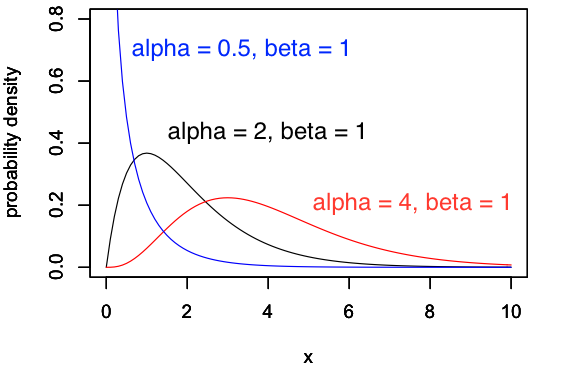
この図から、形状母数 \(\alpha\) の値を大きくしていくと、分布のピークが右のほうに移動していることがわかります。
次に、形状母数 \(\alpha = 2\) に固定して、尺度母数 \(\beta\) を変化させてみます。
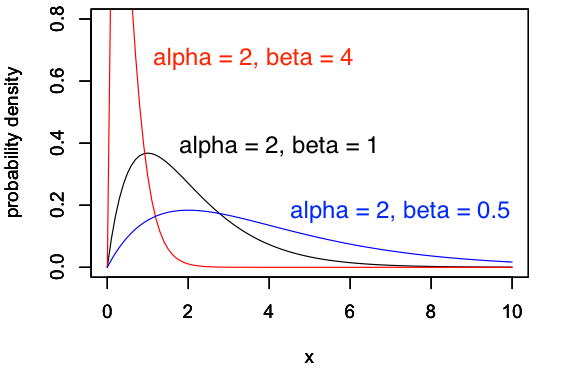
この図から、尺度母数 \(\beta\) の値を大きくしていくと、分布のピークが左のほうに移動していることがわかります。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

