目次(まとめ)
◾️ 正規分布の確率密度関数、積率母関数、特性関数
◾️ 確率変数の変数を置き換えるときには注意が必要
◾️ 正規分布を標準化変換して標準正規分布を得る
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、確率や検定など、統計学を理解する上で欠かすことができない「正規分布」について解説します。
標準化変換を通して「標準正規分布」を得るまでの流れも解説します。
正規分布の確率密度関数、積率母関数、特性関数
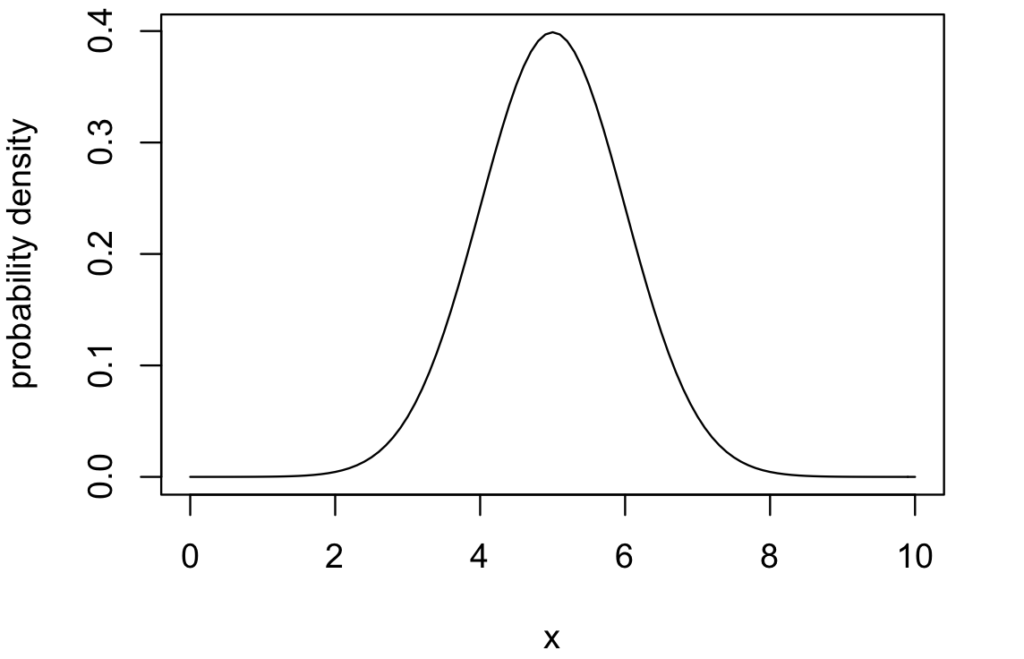
正規分布は、平均\(\mu\)を中心に、分散\(\sigma^2\)のばらつきで描かれる分布です。したがって、上の図で示されるように、見た目も綺麗な分布になります(この図では、\(\mu = 5\)、\(\sigma^2 = 1\)に設定しています)。
ちなみに、上の図で示している正規分布の確率密度関数は、以下のようにRで実行することで得られます(平均と "標準偏差" を指定しているので注意)。
> curve(dnorm(x, 5, 1), 0, 10, xlab = "x", ylab = "probability density")正規分布の確率密度関数は、以下のように得られます。
確率密度関数
$$f_X(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}{\rm exp}\{-\frac{(x - \mu)^2}{2\sigma^2}\}$$
また、平均や分散は、以下の積率母関数や特性関数を用いても取得することができます(詳細はこちらの記事をご覧ください)。平均\(\mu\)、分散\(\sigma^2\)になることを確認できます。
積率母関数
$$M_X(t) = {\rm exp}\{\mu t - \frac{\sigma^2 t^2}{2}\}$$
特性関数
$$\varphi_X(t) = {\rm exp}\{\mu it - \frac{\sigma^2 t^2}{2}\}$$
確率変数の変数を置き換えるときには注意が必要
一般に、確率変数の変数を違う変数に置き換える操作を「変数変換」と呼びますが、そのときには以下のような関係を認識しておく必要があります。
いま、確率変数\(X\)の確率密度関数を\(f_X(x)\)とします。
ここで、\(X\)に何らかの操作をして、確率変数\(Y\)に置き換えることを考えます。数学的には、\(Y = g(X)\)と書きます。逆関数を用いて書くと、\(X = g^{-1}(Y)\)となります。
細かい条件は省きます(詳細は参考文献などをご覧ください)が、\(Y\)の確率密度関数は次のように与えられます。
$$f_Y(y) = f_X(g^{-1}(y))|\frac{{\rm d}}{{\rm d}y} g^{-1}(y)| \qquad \qquad (*)$$
正規分布を標準化変換して標準正規分布を得る
ここでは、正規分布の確率変数\(X\)を、\(Z = \frac{X - \mu}{\sigma}\)という操作をして、確率変数\(Z\)に置き換えることを考えます。
数学的に書くと、\(z = \frac{x - \mu}{\sigma} = g(x)\)と置いて \(g^{-1}(z) = \sigma z + \mu\)となり、\(\frac{{\rm d}}{{\rm d} z} g^{-1}(z) = \sigma\)となります。
これらの情報を、式\((*)\)に当てはめて、正規分布の確率密度関数を用いると、以下のようになります。
$$f_Z(z) = f_X(g^{-1}(z))|\frac{{\rm d}}{{\rm d}z} g^{-1}(z)| = \frac{1}{\sqrt{2\pi}}{\rm exp}\{-\frac{z^2}{2}\}$$
これが標準正規分布の確率密度関数になっています。
確率密度関数
$$\phi(z) = \frac{1}{\sqrt{2\pi}}{\rm exp}\{-\frac{z^2}{2}\}$$
積率母関数
$$M_Z(t) = {\rm exp}\{\frac{t^2}{2}\}$$
特性関数
$$\varphi_Z(t) = {\rm exp}\{-\frac{t^2}{2}\}$$
標準正規分布では、平均\(\mu = 0\)、分散\(\sigma^2 = 1\)になります。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

