目次(まとめ)
◾️ 標本平均の期待値と分散を算出する
◾️ 尤度方程式を立てて最尤推定量を算出する
◾️ フィッシャー情報量は、対数尤度関数の2階微分を用いて算出する
◾️ 参考文献
◾️ 関連記事
こんにちは、みっちゃんです。
今回の記事では、2012年に行われた統計検定1級の統計数理の問題(問3)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
この問題では、指数分布にしたがう確率変数をとりあげ、パラメータの最尤推定量やフィッシャー情報量の算出が求められています。
標本平均の期待値と分散を算出する
いま、\(n\) 個の確率変数 \(X_1, X_2, ..., X_n\) が、互いに独立にパラメータ \(\lambda\) の指数分布にしたがうとします(指数分布についてはこちらの記事をご参照ください)。
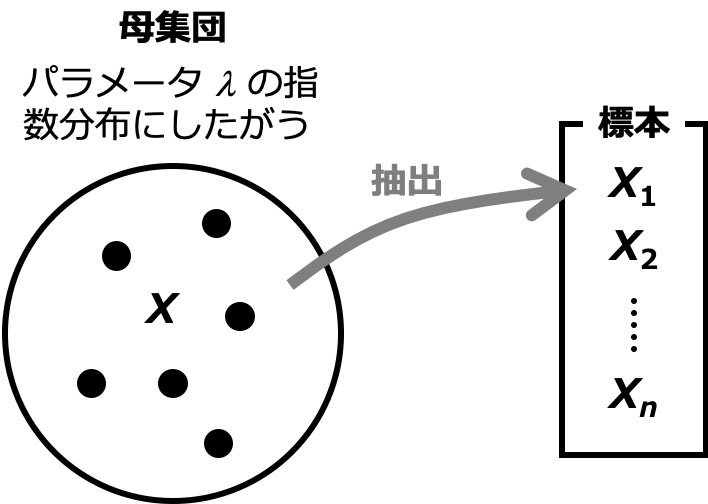
指数分布にしたがう確率変数 \(X\) の平均(期待値)および分散は、以下のように得られます。
$$E[X] = \frac{1}{\lambda}V[X] = \frac{1}{\lambda^2}$$
よって、\(n\) 個の標本について、標本平均 \(\overline{X}\) の平均(期待値)および分散は、以下のように得られます。
$$E[\overline{X}] = \frac{1}{\lambda}V[\overline{X}] = \frac{1}{n}\frac{1}{\lambda^2}$$
つまり、標本平均の平均(期待値)は母集団の平均に一致し、標本平均の分散は母集団の分散をサンプル数 \(n\) で割った値に一致します。
尤度方程式を立てて最尤推定量を算出する
以前の記事で紹介したように、最尤法によってパラメータの最尤推定量を算出する場合には、尤度関数を立てる必要があります。
尤度関数は、確率(密度)関数の積として表されるので、以下のようになります。
確率(密度)関数
$$f_X(x) = \lambda {\rm exp}\{-\lambda x\} \qquad (x \geq 0)$$
尤度関数
$$\begin{eqnarray}L(\lambda) &=& \prod_{i = 1}^n \lambda {\rm exp}\{-\lambda x_i\}\\&=& \lambda^n {\rm exp} \{-\lambda \sum_{i = 1}^n x_i\} \end{eqnarray}$$
尤度関数に対して、両辺対数をとることにより、以下のように対数尤度関数を取得することができます。
$$l(\lambda) = {\rm log} L(\lambda) = n {\rm log} \lambda - \lambda \sum_{i = 1}^n x_i$$
対数尤度関数をパラメータ \(\lambda\) で微分します。
$$\frac{\partial l(\lambda)}{\partial \lambda} = \frac{n}{\lambda} - \sum_{i = 1}^n x_i $$
この式をゼロと置くことで、尤度方程式を立て、最尤推定量を算出することができます。
尤度方程式
$$\frac{n}{{\hat \lambda}} - \sum_{i = 1}^n x_i = 0$$
最尤推定量
$${\hat \lambda} = \frac{n}{\sum_{i = 1}^n x_i}$$
フィッシャー情報量は、対数尤度関数の2階微分を用いて算出する
対数尤度関数をパラメータ \(\lambda\) で2階微分すると、以下のようになります。
$$\frac{\partial^2 l(\lambda)}{\partial \lambda^2} = -\frac{n}{\lambda^2}$$
以前の記事で紹介したように、フィッシャー情報量は、対数尤度関数の2階微分の期待値の負値になります。
したがって、フィッシャー情報量 \(i_n(\lambda)\) は、以下のように得られます。
$$i_n(\lambda) = \frac{n}{\lambda^2}$$

