目次(まとめ)
◾️ 和集合と積集合の関係を理解する
◾️ ボンフェローニ補正により有意水準を調整する
◾️ さまざまな多重比較検定の方法が存在する
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、2013年に行われた統計検定1級の統計応用の医薬生物学分野の問題(問4)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
この問題では、1つの臨床試験で2つの評価項目(エンドポイント)に関する仮説の検証を行うことが考えられています。
和集合と積集合の関係を理解する
いま、それぞれの評価項目に対する帰無仮説を \(H_1\)、\(H_2\) とします。
さらに、"第1種の誤り" を考えるため、\(H_1\) が正しいときに \(H_1\) を誤って棄却してしまう事象を \(E_1\)、\(H_2\) が正しいときに \(H_2\) を誤って棄却してしまう事象を \(E_2\) とします(第1種の誤りについては、こちらの記事をご覧ください)。
ここで、"有意水準" つまり "第1種の誤りの確率" を \(\alpha\) とおき、以下のような状況を考えます。
$${\rm Pr}(E_1) = \alpha{\rm Pr}(E_2) = \alpha$$
この状況では、2つの帰無仮説 \(H_1\) と \(H_2\) のそれぞれについて、有意水準 \(\alpha\) での検証を行うことになります。
この問題ではまず、\({\rm Pr}(E_1 \cup E_2) \geq \alpha\) が成り立つことを求める必要があります。
\(E_1 \cup E_2\) をベン図で図示すると、以下のようになります。
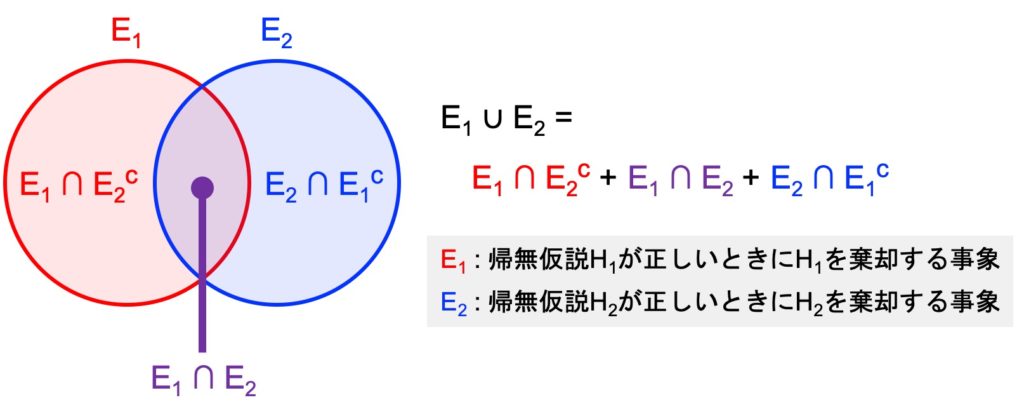
$$\begin{eqnarray}E_1 \cup E_2 &=& E_1 \cap E_2^c + E_1 \cap E_2 + E_2 \cap E_1^c \\&=& E_1 + E_2 \cap E_1^c \\&=& E_1 \cap E_2^c + E_2\end{eqnarray}$$
この関係から、確率は以下のようになります。
$$\begin{eqnarray}{\rm Pr}(E_1 \cup E_2) &=& {\rm Pr}(E_1 \cap E_2^c) + {\rm Pr}(E_1 \cap E_2) + {\rm Pr}(E_2 \cap E_1^c)\\ &=& {\rm Pr}(E_1) + {\rm Pr}(E_2 \cap E_1^c) = \alpha + {\rm Pr}(E_2 \cap E_1^c) \geq \alpha \\&=& {\rm Pr}(E_1 \cap E_2^c) + {\rm Pr}(E_2) = {\rm Pr}(E_1 \cap E_2^c) + \alpha \geq \alpha\end{eqnarray}$$
したがって、\({\rm Pr}(E_1 \cup E_2) \geq \alpha\) が成り立つことがわかります(等号が成立するのは \(E_1 = E_2\) のときです)。
ボンフェローニ補正により有意水準を調整する
この問題では \({\rm Pr}(E_1 \cup E_2) \leq 2\alpha\) という関係に注目しています。
この関係は、以下に示す「確率の加法定理」から簡単に導くことができます。
$${\rm Pr}(E_1 \cup E_2) = {\rm Pr}(E_1) + {\rm Pr}(E_2) - {\rm Pr}(E_1 \cap E_2)$$
この関係が意味するのは、\(E_1\) または \(E_2\) が起こる確率は \(2\alpha\) 以下になる、つまり、帰無仮説 \(H_1\) が誤って棄却される事象、または、帰無仮説 \(H_2\) が誤って棄却される事象が起こる確率が \(2\alpha\) 以下になるということです。
しかし、もともと、それぞれの帰無仮説に対する有意水準(誤って棄却される確率)を \(\alpha\) にしていたのに、\(2\alpha\) にあがってしまっていることがわかります。
つまり「多重性の問題」が生じています(詳しくはこちらの記事をご覧下さい)。
この問題では、有意水準 \(0.05\) の検定を2重に行っているので、ボンフェローニ補正(詳しくはこちらの記事をご覧下さい)により、共通の有意水準を \(0.05/2 = 0.025\) として与えれば、\({\rm Pr}(E_1 \cup E_2) \leq \alpha\) となります。
さまざまな多重比較検定の方法が存在する
この問題では、2つの帰無仮説 \(H_1\) と \(H_2\)、対応する対立仮説 \({\overline H_1}\) と \({\overline H_2}\) を考えています。
起こる可能性がある帰無仮説 \(H_1 \cup H_2\) を考えると、\(H_1 \cap {\overline H_2}\)、\(H_1 \cap H_2\)、\(H_2 \cap {\overline H_1}\) の3通りあることがわかります(上に示したベン図が参考になります)。
(1) \(H_1 \cap H_2\)
:この積集合が示すのは、2つの帰無仮説が同時に成り立つということなので、この積集合を棄却するためには、\(H_1\) に対する \(p\) 値である \(p_1\) が \(\alpha/2\) 以下、または、\(H_2\) に対する \(p\) 値である \(p_2\) が \(\alpha/2\) 以下である必要があります。つまり、\(2p_1 \leq \alpha\) または \(2p_2 \leq \alpha\) です。
(2) \(H_1 \cap {\overline H_2}\)
:この積集合が示すのは、2つの帰無仮説のうち \(H_1\) だけ成り立つということなので、この積集合を棄却するには、\(H_1\) に対する \(p\) 値である \(p_1\) が \(\alpha\) 以下である必要があります。
(3) \(H_2 \cap {\overline H_1}\)
:この積集合が示すのは、2つの帰無仮説のうち \(H_2\) だけ成り立つということなので、この積集合を棄却するには、\(H_2\) に対する \(p\) 値である \(p_2\) が \(\alpha\) 以下である必要があります。
これらをまとめて、\(H_1\) が棄却される条件を考えてみます。
(1)から、\(2p_1\) または \(2p_2\) が \(\alpha\) 以下になると棄却されるので、\(2p_1\) または \(2p_2\) の小さい方が \(\alpha\) 以下になると棄却されることになります。
また、(2)から、\(p_1\) が \(\alpha\) 以下でも棄却されることがわかります。
したがって、\({\rm max}\{{\rm min}(2p_1, 2p_2), p_1\} \leq \alpha\) のときに、\(H_1\) が棄却されることになります。
同じように、\(H_2\) が棄却される条件も算出することができます。

