目次(まとめ)
◾️ すべての確率密度関数を掛け合わせて尤度関数を求める
◾️ デルタ法をつかって漸近分散を算出する
◾️ 検定を行う場合には標準正規分布を使えるような確率変数を設計する
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、2013年に行われた統計検定1級の統計応用の医薬生物学分野の問題(問2)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
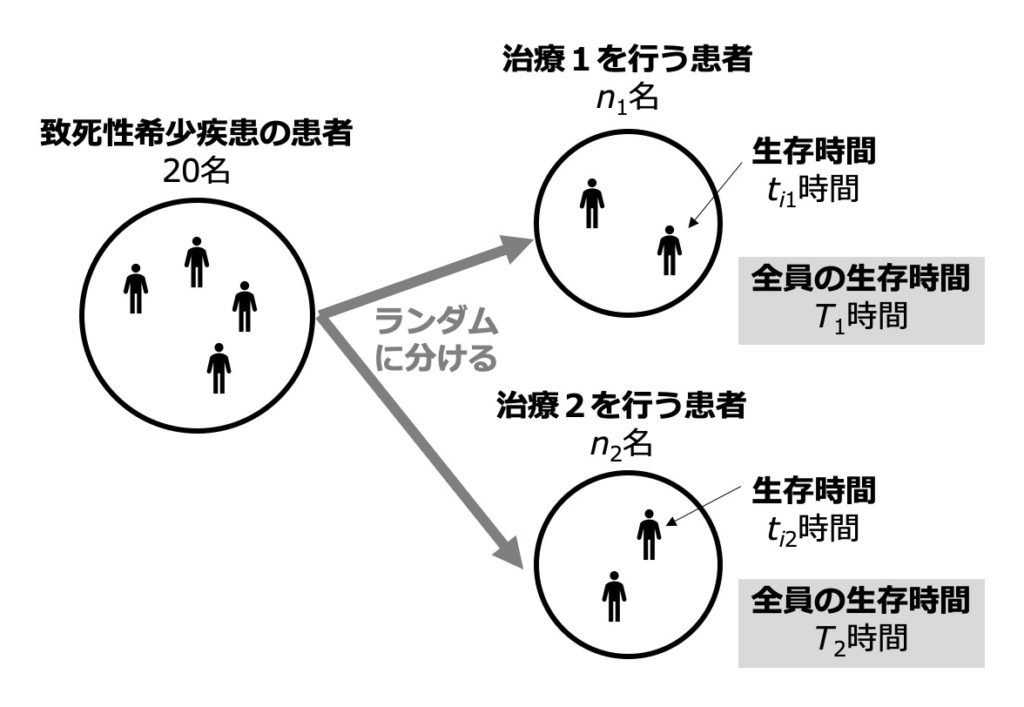
この問題では、致死性の希少疾患に対して2つの治療を行ったときに、その効果を追跡した生存時間解析が考えられています。
すべての確率密度関数を掛け合わせて尤度関数を求める
この問題では、それぞれの治療を行う患者の生存時間が、パラメータ \(\lambda\) の指数分布にしたがうと仮定しています(指数分布についてはこちらの記事をご参照ください)。
したがって、治療1を受ける患者群、治療2を受ける患者群、それぞれの群の患者 \(i\) に対して、以下のような確率密度関数が与えられます。
$$f_1 (t_{i1}) = \lambda_1 {\rm exp} \{- \lambda_1 t_{i1}\}f_2 (t_{i2}) = \lambda_2 {\rm exp} \{- \lambda_2 t_{i2}\}$$
この問題では「尤度関数」を求める必要がありますが、尤度関数は同時確率密度関数に対応するので、以下のようになります。つまり、すべての患者に対する確率密度関数をすべて掛け合わせるだけです。
$$L = \prod_{i = 1}^{n_1} \lambda_1 {\rm exp} \{- \lambda_1 t_{i1}\} \prod_{i = 1}^{n_2} \lambda_2 {\rm exp} \{- \lambda_2 t_{i2}\}$$
また、尤度関数を対数尤度関数に変換して、偏微分することで尤度方程式を構築し、それを解くことで「最尤推定量」やその「漸近分散」を求めることができます。
詳しくは、以下の記事をご参照ください。
- 最尤推定量の算出について:こちらの記事
- 漸近分散の算出について:こちらの記事
デルタ法をつかって漸近分散を算出する
この問題では、最尤推定量 \({\hat \lambda_1}\) と \({\hat \lambda_2}\) を対数変換した \({\rm log} {\hat \lambda_1}\) と \({\rm log} {\hat \lambda_2}\) の漸近分散が求められています。
この漸近分散は、デルタ法と呼ばれる定理により、「"微分値の2乗"と"分散"の積」で表現されるので、以下のようになります(デルタ法については、こちらの記事をご参照ください)。
$$V[{\rm log} {\hat \lambda_1}] \approx {({\rm log} {\hat \lambda_1})'}^2 V[{\hat \lambda_1}]V[{\rm log} {\hat \lambda_2}] \approx {({\rm log} {\hat \lambda_2})'}^2 V[{\hat \lambda_2}]$$
ここで、\(V[{\hat \lambda_1}] = \frac{\lambda_1^2}{n_1}\)、\(V[{\hat \lambda_2}] = \frac{\lambda_2^2}{n_2}\) となる(詳しくはこちらの記事をご覧ください)ので、以下のように変換できます。
$$V[{\rm log} {\hat \lambda_1}] \approx (\frac{1}{\lambda_1})^2 \frac{\lambda_1^2}{n_1} = \frac{1}{n_1}V[{\rm log} {\hat \lambda_2}] \approx (\frac{1}{\lambda_2})^2 \frac{\lambda_2^2}{n_2} = \frac{1}{n_2}$$
検定を行う場合には標準正規分布を使えるような確率変数を設計する
この問題では、推定量 \({\rm log} {\hat \lambda_1}\)、\({\rm log} {\hat \lambda_2}\) が近似的に正規分布にしたがうと仮定しています。
いま帰無仮説として、\(\lambda_1 = \lambda_2\) を設定した場合、この仮説が正しいかどうかを検定するための統計量は以下のようになります。
$$Z = \frac{{\rm log} {\hat \lambda_1} - {\rm log} {\hat \lambda_2}}{\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}$$
問題で与えられている数値を当てはめることで、標準正規分布表から仮説検定を行うことができます。

