目次(まとめ)
◾️ 感染症が流行する過程をあらわすSIRモデル
◾️ Rをつかって、微分方程式モデルのシミュレーションをする
こんにちは、みっちゃんです。
今回の記事では、感染症が蔓延したときに感染者や回復者の数が時間経過とともにどのように変化するのかを表現する「SIRモデル」を使って、簡単なシミュレーションをする方法を紹介します。
感染症が流行する過程をあらわすSIRモデル
SIRモデルとは、感染症が流行する過程を、時間経過とともにシミュレーションするために、約100年前(1927年)に提案された数理モデルです。
SIRは「Susceptible(感受性保持者)」「Infected(感染者)」「Recovered(免疫保持者)」の頭文字に対応しています。
感受性保持者(S):今後感染症にかかる可能性がある人
感染者(I):感染している人
免疫保持者(R):感染したのち回復して、ウイルスなどに対する免疫をもった人
シミュレーション対象となる人は、"S" か "I" か "R" に割り当てられることになるので、例えば、100人の住民がいる村に注目してシミュレーションする場合には、10人が感染症に感染していて、80人が今後感染症にかかる可能性があり、回復した人は10人、といった状況に対応します。
「SIRモデル」は、以下のような連立微分方程式として定義されます。単位時間(例えば、1時間)あたりに人数がどのぐらい変化するのかを示しています。
$$\begin{eqnarray}\frac{dS(t)}{dt} &=& -\beta S(t)I(t)\qquad(1)\\\frac{dI(t)}{dt} &=& \beta S(t)I(t) - \gamma I(t)\qquad(2)\\\frac{dR(t)}{dt} &=& \gamma I(t)\qquad(3)\end{eqnarray}$$
ここで、\(t\) は時間を意味するので、\(S(t)\) は時間経過とともに変化する感受性保持者の数、\(I(t)\) は時間経過とともに変化する感染者の数、\(R(t)\) は時間経過とともに変化する免疫保持者の数を指します。
また、\(\beta\) は "感染率" を示すパラメータ、\(\gamma\) は "回復率" を示すパラメータです。\(\beta\) の値が大きければ、感染力が高い感染症であることを示し、\(\gamma\) の値が大きければ、回復しやすい感染症であることを示します。
\((1)\) 式は、感受性保持者の数の時間変化を表していますが、マイナスの項のみで表されていることから、感受性保持者数は時間経過とともに減少していくようにモデル化されていることがわかります。また、その減少度合いは、感受性保持者と感染者の数によって決まるようにモデル化されています。これは、感染症が蔓延する状況において、感染していない人は減少していくこと、感染者が周りに多ければ減少速度は早くなること、を意味しています。
\((2)\) 式は、感染者の数の時間変化を表しています。\((1)\) 式と異なり、プラスの項とマイナスの項で表されていることから、感染者数の時間変化は、2つの項のバランスによって決まるようにモデル化されていることがわかります。プラスの項は、感染により感染者数が増えていくこと、マイナスの項は、回復により感染者数が減っていく(回復者数が増えていく)ことを意味しています。単位時間あたりで、感染者数が回復者数より大きければ、全体として感染者が増えていきますが、感染者数が回復者数より小さければ、全体として感染者が減っていきます。
\((3)\) 式は、免疫保持者の数の時間変化を表していますが、プラスの項のみで表されていることから、免疫保持者数は時間経過とともに増加していくようにモデル化されていることがわかります。また、その増加度合いは、感染者の数によって決まるようにモデル化されています。これは、感染者が多ければ回復頻度は高くなること、を意味しています。
Rをつかって、微分方程式モデルのシミュレーションをする
無料で使える統計解析ソフトウェアのRは、SIRモデルのような微分方程式モデルのシミュレーションにも使うことができます(Rについての詳細はこちらの記事をご参照ください)。
ここでは、"deSolve" パッケージを使用するので、以下のようにインストールして使える状態にします。
> install.packages("deSolve")
> library(deSolve)SIRモデルをシミュレーションするためには、以下のようなスクリプトを実行します。
#モデルのパラメータを適当に設定(SIRモデルでは、betaとgammaです)
parameters <- c(beta = 0.2, gamma = 0.7)
#S, I, Rに対して最初に割り振る人数を設定(初期値の設定)
initial <- c(s = 80, i = 10, r = 10)
#時間点を指定(ここでは、0, 0.01, 0.02, 0.03, ..., 10、に指定しています)
times <- seq(0, 10, 0.01)
#数理モデルの定義
SIR_model <- function(t, state, parameters) {
with(as.list(c(state, parameters)), {
ds <- -beta * s * i #(1)式に対応
di <- beta * s * i - gamma * i #(2)式に対応
dr <- gamma * i #(3)式に対応
list(c(ds, di, dr))
})
}
#ODE(Ordinary Differential Equation)関数を使って計算
out <- ode(y = initial, times = times, func = SIR_model, parms = parameters)計算が終わると、計算結果が "out" という変数に保存されています。
> head(out)
time s i r
[1,] 0.00 80.00000 10.00000 10.00000
[2,] 0.01 78.29064 11.63377 10.07560
[3,] 0.02 76.35142 13.48520 10.16338
[4,] 0.03 74.16806 15.56701 10.26493
[5,] 0.04 71.73074 17.88738 10.38188
[6,] 0.05 69.03569 20.44840 10.51591計算によって得られた結果をプロットするには、例えば、以下のように実行します。
> matplot(out[,1], out[,2:4], type="l", xlim=c(0,10), col = c("black", "red", "blue"))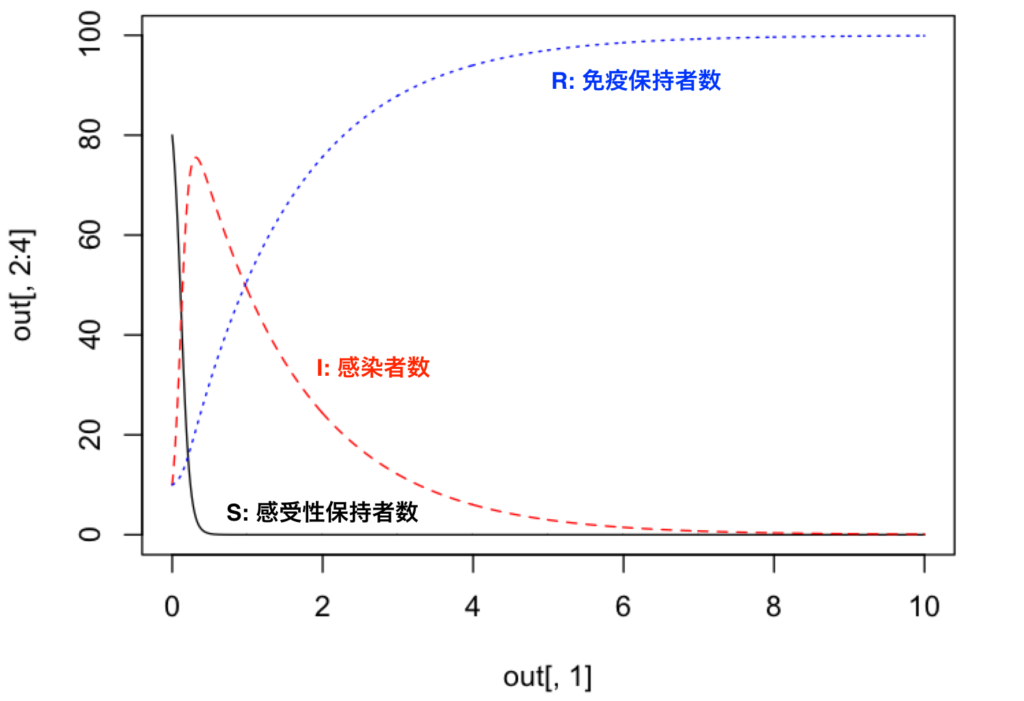
この図から、感染率パラメータ \(\beta = 0.2\)、回復率パラメータ \(\gamma = 0.7\) としたときに、初期の段階で感染者数が急激に増加して、その後、回復者が増えていく様子がわかります。
仮に、回復率パラメータ \(\gamma\) を \(0.1\) として、回復が難しい場合のシミュレーションをすると以下のような挙動が得られます。
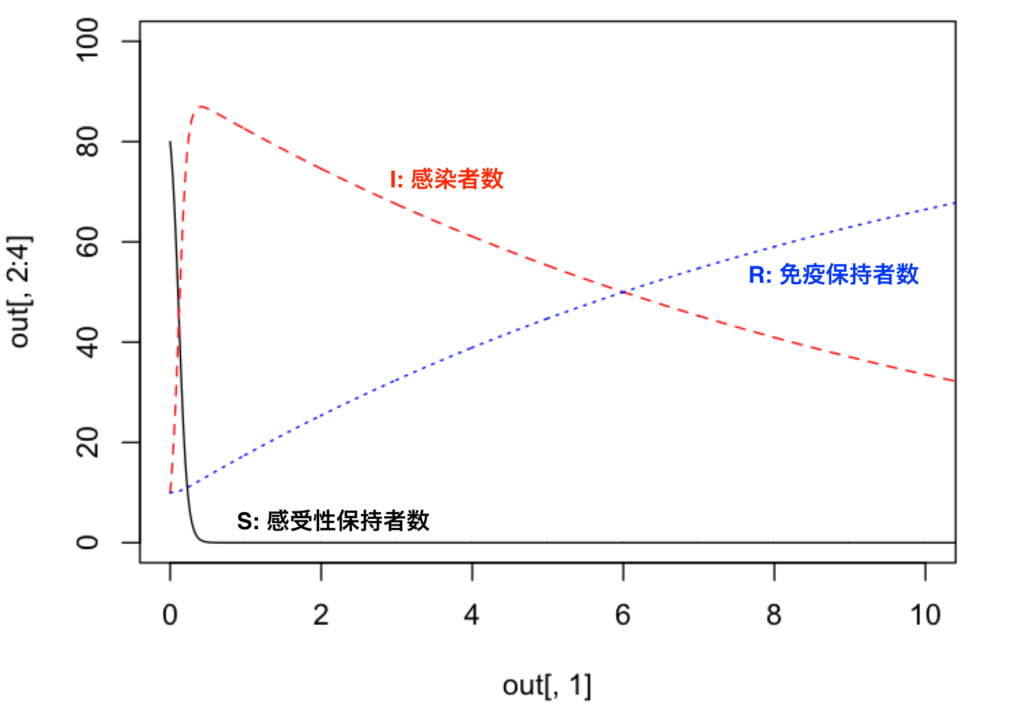
この結果から、感染者数がなかなか減少しないことがわかります。
つまり、感染率や回復率に対するパラメータに対して、すでにわかっている統計値などを活用して適切な値を設定することが重要になります。

