目次(まとめ)
◾️ 記述統計と推測統計は、母集団の確率分布を考慮するかどうかという点で異なる
◾️ 推測統計では、標本の平均や分散を考える
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、母集団から選び出した標本を使って、母集団の特性を予測するための「推測統計」のアプローチを紹介します。
記述統計と推測統計は、母集団の確率分布を考慮するかどうかという点で異なる
ここでは、日本人の身長を調べて、日本人の身長の平均や身長のばらつき(分散)を知りたいという状況を考えます。
しかし、全ての日本人について、身長の値を取得することは困難です。
そこで、全ての日本人の中から、日本人を複数人選んで、その選ばれた人の身長を調査して、全ての日本人のデータを予想するということを行います。
専門用語を使って表現すると「母集団(例:全ての日本人)から標本(例:選ばれた日本人)を選んで、その標本を使って母集団の特性を調べる」ということになります。
ここで、標本をどのように使って母集団の特性を調べるのかによって「記述統計」と「推測統計」という考え方があります。
記述統計
標本の平均や分散を計算して母集団の特性を調べます。この考え方では、母集団がどのような確率分布にしたがうかは考えません。身長の例で言うと、選ばれた人の身長について平均や分散を計算するということです。
推測統計
母集団は何らかの確率分布にしたがっていて、標本の値もその確率分布にしたがう確率変数の実現値であると考えます。身長の例で言うと、全ての日本人の身長の分布が何らかの確率分布(例:正規分布)にしたがっていて、選ばれた人の身長はその確率分布にしたがう確率変数の値であると考えます。
推測統計では、標本の平均や分散を考える
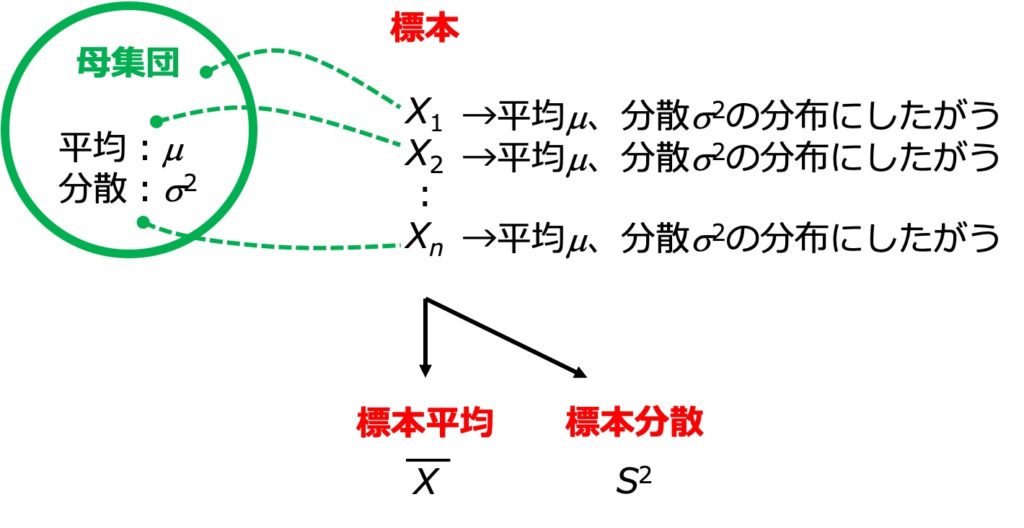
上の図では、平均 \(\mu\)、分散 \(\sigma^2\) の正規分布にしたがう母集団から、\(n\) 個の標本をランダムに抽出することを考えています。
標本についての平均や分散は、それぞれ「標本平均」「標本分散」と呼ばれます。
標本平均 \(\overline{X}\)
$$\overline{X} = \frac{1}{n} \sum_{i = 1}^{n}X_i$$
標本分散 \(S^2\)
$$S^2 = \frac{1}{n} \sum_{i = 1}^{n} (X_i - \overline{X})^2$$
ここで、標本平均の平均(期待値)と分散は、以下のように計算することができます。
標本平均の平均(期待値)
$$E[\overline{X}] = E[\frac{1}{n} \sum_{i = 1}^{n}X_i] = \frac{1}{n} \sum_{i = 1}^{n} E[X_i] = \frac{1}{n} n\mu = \mu$$
標本平均の分散
$${\rm Var}(\overline{X}) = {\rm Var}(\frac{1}{n} \sum_{i = 1}^{n}X_i) = \frac{1}{n^2} {\rm Var}(\sum_{i = 1}^{n}X_i) = \frac{1}{n^2} \sum_{i = 1}^{n}{\rm Var}(X_i) = \frac{1}{n^2}n\sigma^2 = \frac{\sigma^2}{n}$$
標本平均の分散の計算においては、\(X_1, X_2, ..., X_n\) が独立のときに成り立つ以下の関係を使用しています。
$${\rm Var}(\sum_{i=1}^{n} a_i X_i) = \sum_{i=1}^{n} a_i^2 {\rm Var}(X_i)$$
また、標本分散の平均(期待値)は、以下のように計算することができます。
標本分散の平均(期待値)
$$E[S^2] = E[\frac{1}{n} \sum_{i = 1}^{n} (X_i - \overline{X})^2] = \frac{1}{n} (n-1) \sigma^2$$
このことから、母集団の分散は \(\sigma^2\) であるのにも関わらず、標本の分散に対して期待できる値は \(\sigma^2\) にならないことがわかります。
逆にいうと、標本分散を以下のように定義しておけば、標本の分散に対して期待できる値が母集団の分散 \(\sigma^2\) と一致するようになります。
$$V^2 = \frac{1}{n-1} \sum_{i = 1}^{n} (X_i - \overline{X})^2$$
この \(V^2\) という分散を、不偏分散と呼びます。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

