目次(まとめ)
◾️ 仮説検定では「帰無仮説」と「対立仮説」という2つの仮説について考える
◾️ 標本から検定統計量を準備して仮説検定に用いる
◾️ 帰無仮説を棄却してしまう確率を有意水準を使って設定する
◾️ 参考文献
こんにちは、みっちゃんです。
これまでの記事において、母集団がしたがう確率分布のパラメータを推定するための「点推定」について、以下に示す3つの手法を紹介しました。
□ モーメント法(詳しくはこちら)
□ 最尤法(詳しくはこちら)
□ ベイズ法(詳しくはこちら)
今回の記事では「点推定」と同様に重要な推定法である「仮説検定」について紹介します。
仮説検定では「帰無仮説」と「対立仮説」という2つの仮説について考える
仮説検定では「仮説」を使って統計的な検定を行います。
「仮説」とは、文字通り「仮の説」で、広辞苑によれば「自然科学その他で、一定の現象を統一的に説明しうるように設けた仮定。ここから理論的に導きだした結果が観察・計算・実験などで検証されると、仮説の域を脱して一定の限界内で妥当する法則や理論となる。」とされています。
統計的な仮説検定では、何らかの仮説を設定して、それが統計的に正しいと言えるのか検証していくことになります。
その際「帰無仮説」と「対立仮説」という2つの仮説を考えます。
これらの仮説は、お互いに排反に、つまり、まったく逆のことを主張する仮説になっています。
例えば、小学6年生に対して行われた身体測定の結果で、「全国の生徒の平均体重」と「ある小学校の生徒の体重」を比較したいとします。
このとき、一般に、「帰無仮説」と「対立仮説」は以下のように設定されます。
帰無仮説:全国の生徒の平均体重とある小学校の生徒の平均体重は "等しい"
対立仮説:全国の生徒の平均体重とある小学校の生徒の平均体重は "等しくない"
考えてみるといいかもしれませんが、ある小学校の生徒だけ体重が重いといった状況は考えづらいため、帰無仮説は、限りなく確からしい仮説です。
このように、受け入れられると予想される仮説を「帰無仮説」とするのが普通です(「等しくない」という仮説は、「等しくない」度合いがさまざまであることから、帰無仮説にするには不適とも言えます)。
標本から検定統計量を準備して仮説検定に用いる
仮説検定では、標本 \(X_1, X_2, ..., X_n\) を使って「検定統計量」と呼ばれる統計量を準備します。
一般に、\(T\) と表され、\(X_1, X_2, ..., X_n\) の関数になります。
この検定統計量 \(T\) が、帰無仮説の受容域にあれば帰無仮説が受容され、帰無仮説の棄却域にあれば帰無仮説が棄却されることになります。
帰無仮説を棄却してしまう確率を有意水準を使って設定する
受け入れたい「帰無仮説」ですが、当然、それを受け入れられず、棄却せざるを得ない状況は起こります。
そのときのために、帰無仮説を間違って棄却してしまう確率が \(\alpha\) 以下になるように、帰無仮説を棄却するということが考えられます。
この \(\alpha\) を「有意水準」と呼んでいます。
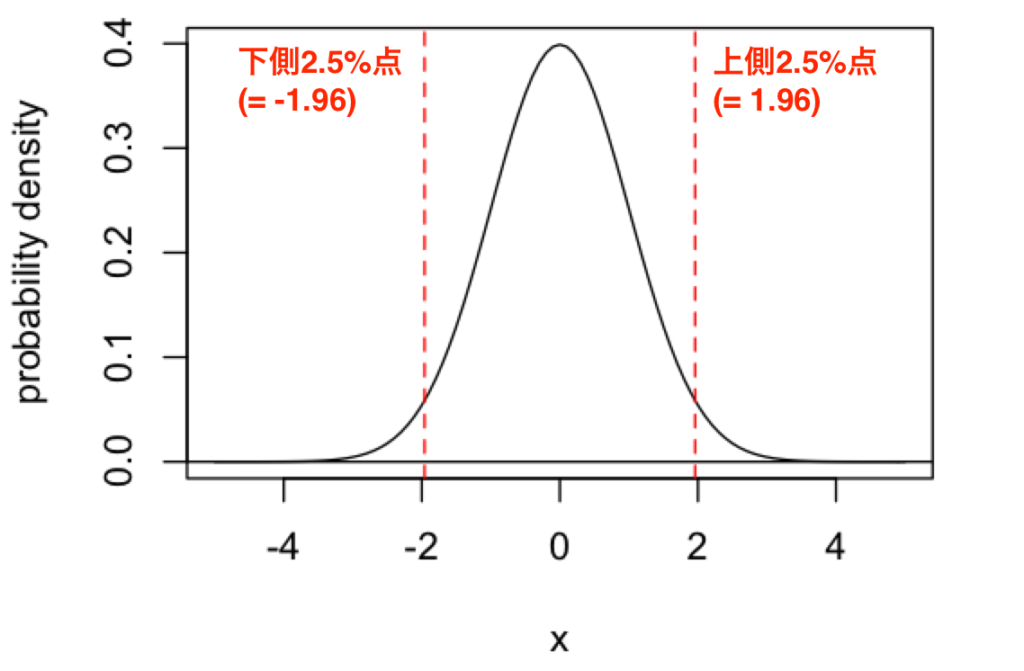
例えば、仮説検定を行う検定統計量が、以下のような標準正規分布にしたがうとき、上側2.5%点や下側2.5%点をつかって、どのようなときに帰無仮説を棄却するかを検討していきます。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

