こんにちは、みっちゃんです。
以前の記事で、2進数などについて紹介しました。
今回の記事では、2進数を用いた四則演算(足し算、引き算、掛け算、割り算)のうち、「掛け算」と「割り算」について紹介したいと思います。
※「足し算」と「引き算」はこちらの記事をご覧ください。
目次(まとめ)
- 掛け算:もとの2進数を左に1つずらすことで「2倍」になる
- 割り算:もとの2進数を右に1つずらすことで「1/2倍」になる
- 四則演算をフル活用して、半端な掛け算/割り算に対応
- 参考文献
掛け算:もとの数字を左に1つずらすことで「2倍」になる
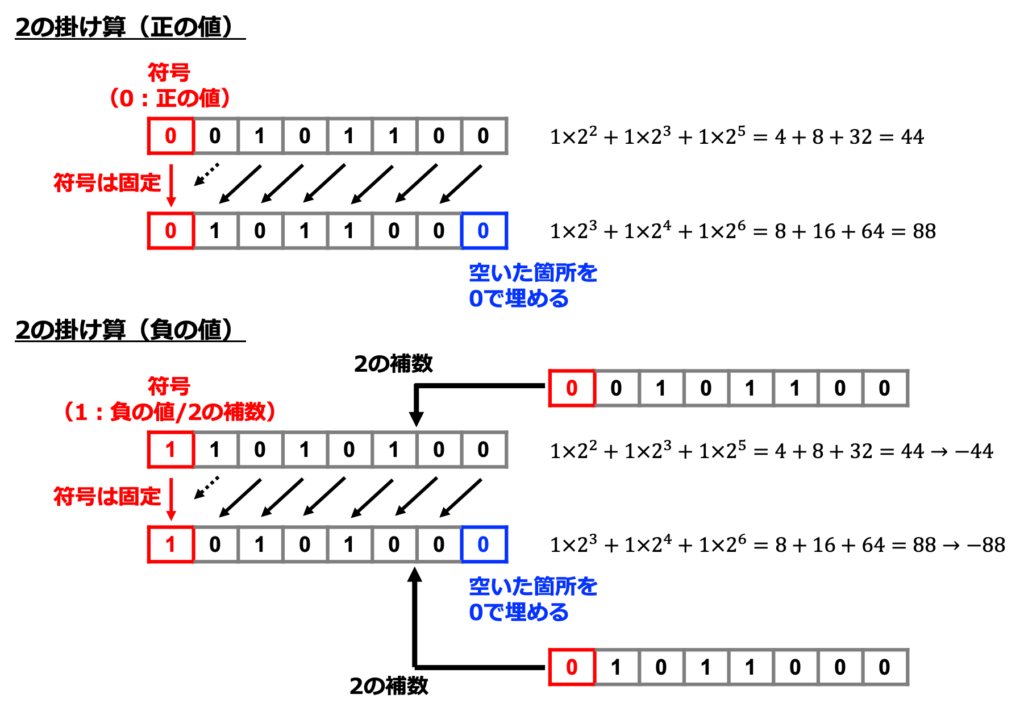
2進数の掛け算の基本は「2倍にする方法を覚える」ことです。
上の図では、8桁(8ビット)の2進数が与えられた時に、2倍する方法を示しています。
一番左のビット(最上位ビット)は、その数値が「正の値」か「負の値」か判別するために使用します。
以前の記事で紹介したように、「負の値」は「2の補数」で表現され、最上位ビットは必ず「1」となります。
図に示しているように「符号を考慮して2進数を2倍にする」ということは「最上位ビットを残したまま、ビットを左に移動させる」ことに対応します。
移動させることにより空いたビットは必ず「0」で埋めます。
割り算:もとの数字を右に1つずらすことで「1/2倍」になる
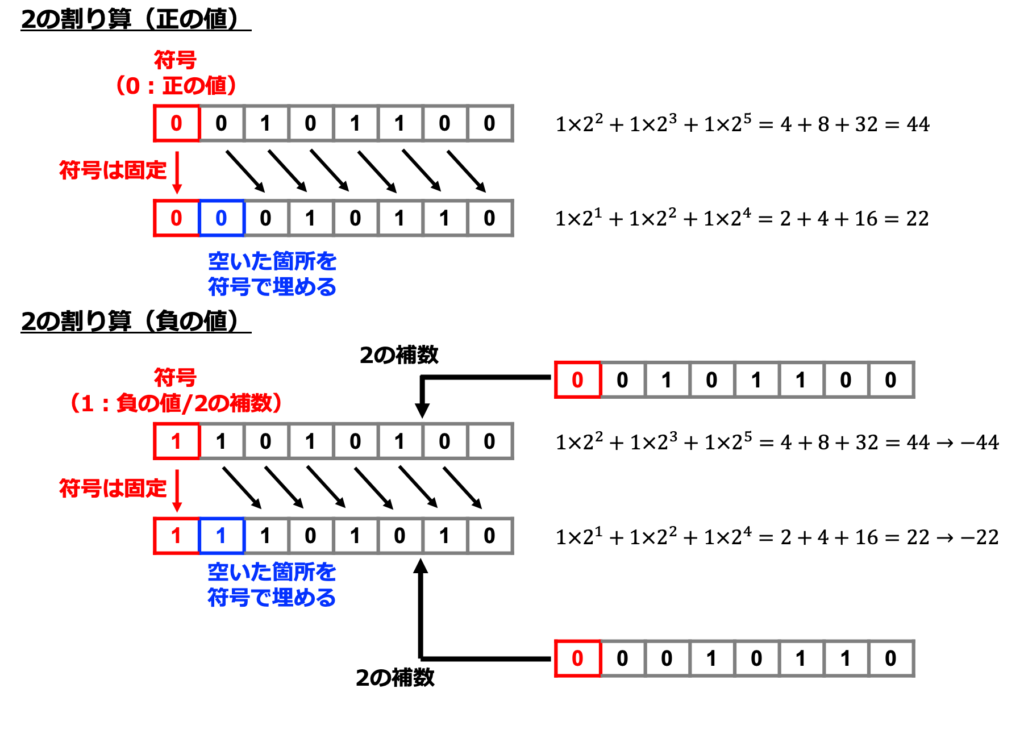
2進数の割り算の基本は「1/2倍にする方法を覚える」ことです。
上の図では、8桁(8ビット)の2進数が与えられた時に、1/2倍する方法を示しています。
掛け算の場合とは対照的に、「符号を考慮して2進数を1/2倍にする」ということは「最上位ビットを残したまま、ビットを右に移動させる」ことに対応します。
移動させることにより空いたビットは必ず「符号」と同じ数字で埋めることに注意が必要です。
これらの計算を試してみる際には、8ビットの2進数が、10進数で最大256までしか表現できないことに注意してください。
計算がうまくいかないと悩む場合には、小さい数字で試してみるといいと思います。
四則演算をフル活用して、半端な掛け算/割り算に対応
上に示したように、2倍すること、1/2倍する(2で割る)ことは、ビットをずらすだけで実現することができます。
それでは「3倍」や「1/3倍」はどうすればいいのでしょうか。
【3倍の例】
3倍は「2倍+1倍」、つまり「\(2^1\)倍した数字」と「\(2^0\)倍した数字」を足すことで実現します。
「010」の3倍であれば、「100」と「010」の足し算で「110」となります(10進数での\(2 \times 3 = 6\)です)。
【1/3倍の例】
1/3倍は、2進数の「11」を、もとの数字から引いて実現します。
「110」の1/3倍であれば、「11」を引いていくわけです。
「11」を1ビット左にずらした「110」を1回引けばいいわけなので「\(2^1\)」となります(10進数での\(6 \div 3 = 2\)です)。
参考文献
きたみりゅうじ「キタミ式イラストIT塾 応用情報技術者」技術評論社

