こんにちは、みっちゃんです。
コンピュータは、電源のオン/オフで「1」「0」を表現して、複雑な処理を行っているため、2進数を使っています。
これを理解するためには、われわれが使っている10進数とうまく切り分けをする必要があります。
今回の記事では、10進数を復習して、2進数/8進数/16進数を理解するアプローチを紹介します。
目次(まとめ)
- 小学校算数をおさらいして10進数で繰り上がりの仕組みを理解する
- 2進数は「2個そろったら繰り上がる」数字
- n進数は「n個そろったら繰り上がる」数字
小学校算数をおさらいして10進数で繰り上がりの仕組みを理解する
みなさん、小学校のときに足し算を習ったと思いますが、そのときに壁になるのが「繰り上がり」だと思います。
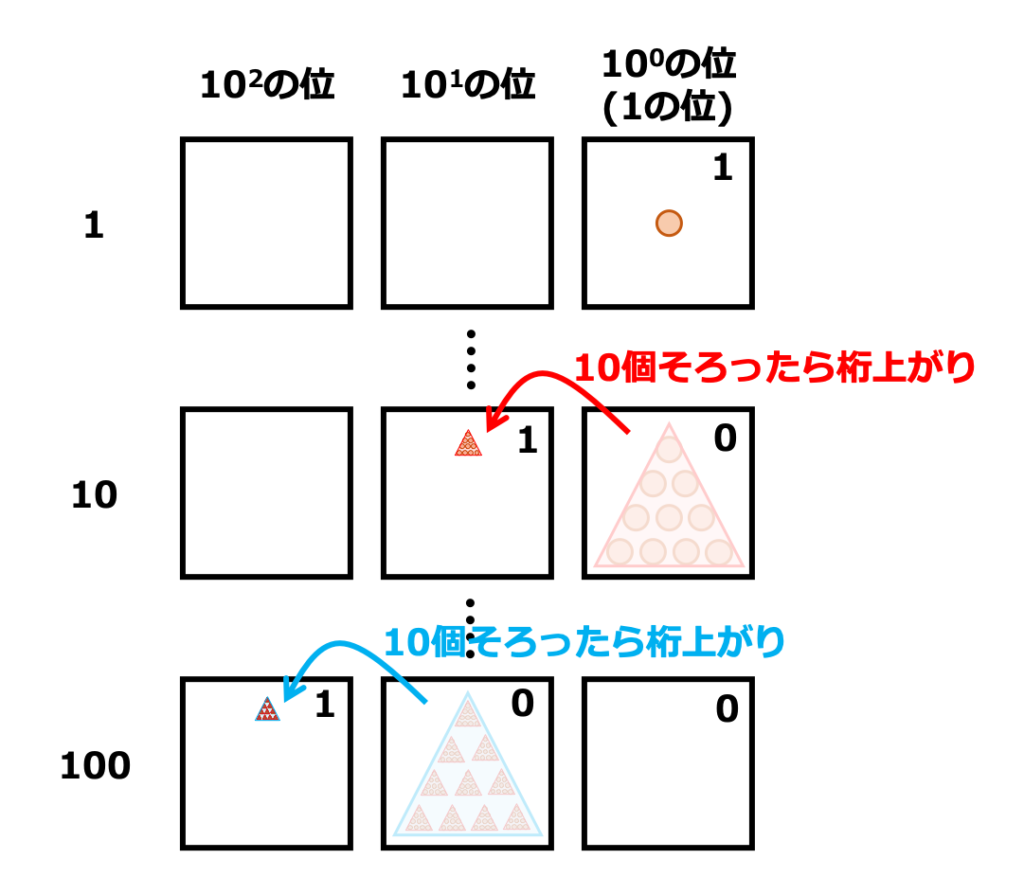
上の図では、1の位(\(10^0\)の位)と10の位(\(10^1\)の位)と100の位(\(10^2\)の位)を示しています。
当然、1の位に1つずつ丸を増やしていき、10個そろったら繰り上がり「10」ができあがることになります。
さらに、「10」が10個そろったら繰り上がり「100」が出来上がります。
このように、10個そろったら繰り上がりを繰り返していくことで表現した数字を「10進数」といいます。
つまり「10個で進む」ということですね。
2進数は「2個そろったら繰り上がる」数字
「10進数」と同じように考えると「2進数」も簡単に理解できます。
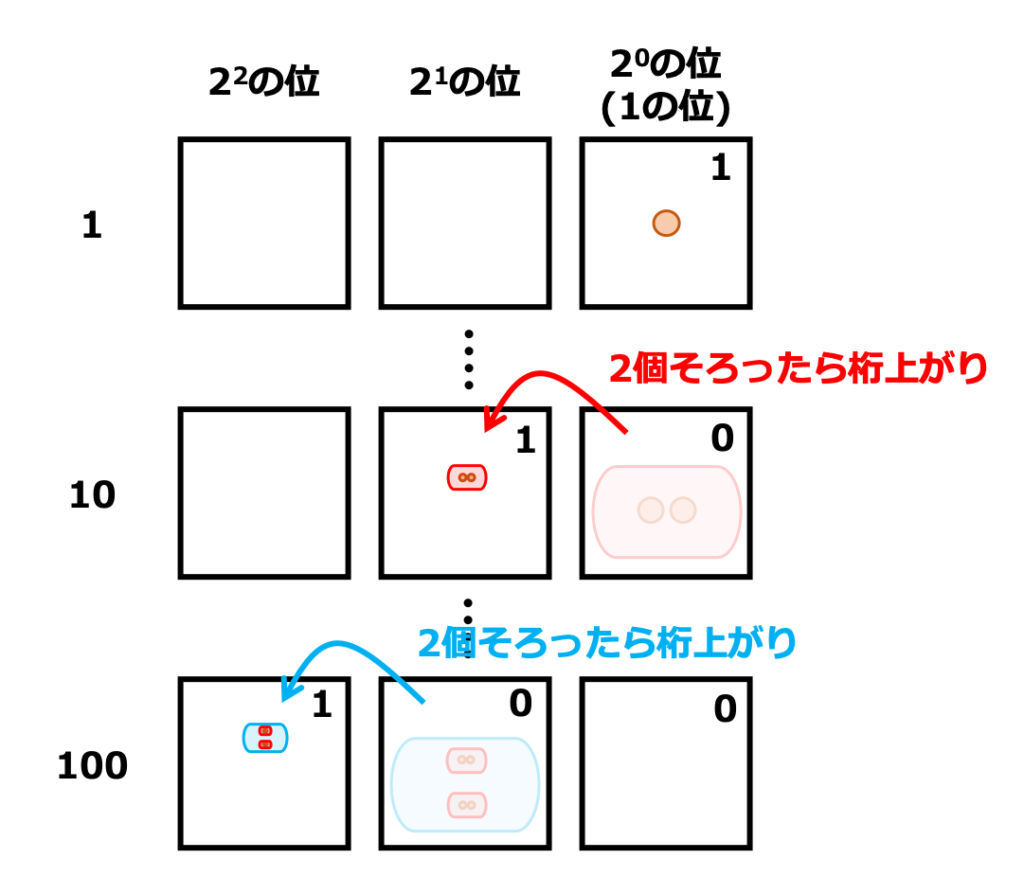
上の図では、1の位(\(2^0\)の位)と2の位(\(2^1\)の位)と4の位(\(2^2\)の位)を示しています。
1の位に1つずつ丸を増やしていき、2個そろったら繰り上がり「10」ができあがることになります。
ただし「10」とは、2進数での「10」なので、10進数ではないということに注意してください。
2進数での「10」を10進数に変換したい場合には、上のボックスをイメージして、以下のように計算します。
$$1 \times 2^1 + 0 \times 2^0 = 2$$
つまり、2進数の「10」は、10進数の「2」を意味します。
n進数は「n個そろったら繰り上がる」数字
コンピュータの分野では、2進数の他にも、よく使われる8進数や16進数があります。
2進数:0, 1
8進数:0, 1, 2, 3, 4, 5, 6, 7
16進数:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
上に示したようなやり方で、これらも簡単に理解することができます。
つまり「8進数」は8個そろったら繰り上がり、「16進数」は16個そろったら繰り上がるような数字です。
例えば、16進数として「132」があったとします。
これは10進数で考えると、\(1 \times 16^2 + 3 \times 16^1 + 2 \times 16^0\)となり「306」を意味していることになります。

