-
目次(まとめ)
- ◾️ 「食べる者」と「食べられる者」の数の変化を表現するロトカ・ヴォルテラの方程式
- ◾️ Rをつかって、微分方程式モデルのシミュレーションをする
- ◾️ 関連記事

「ロトカ・ヴォルテラの方程式」とは、どのような方程式ですか?
「ロトカ・ヴォルテラの方程式」は、捕食者(食べる者)と被食者(食べられる者)の数が、時間とともにどのように変化するのかを表現するための連立微分方程式です。
アメリカの数学者 "ロトカ" さんと、イタリアの数学者 "ヴォルテラ" さんが発案しました。
今回の記事では、「ロトカ・ヴォルテラの方程式」の概要と、Rを使ったシミュレーション方法を紹介します。


「食べる者」と「食べられる者」の数の変化を表現するロトカ・ヴォルテラの方程式
ロトカ・ヴォルテラの方程式は、捕食者(食べる者)と被食者(食べられる者)の数の変化を表現する2つの微分方程式から構成されます。
ここでは、被食者の数を記号 \(x\)、捕食者の数を記号 \(y\) で表現します。
まず、被食者の数の時間変化は時間微分 \(\frac{dx}{dt}\) になるので、以下のような式を立てます。
$$\frac{dx}{dt} = ax - bxy$$
右の辺の最初の項にある "\(ax\)" は、被食者の数を \(a\) 倍していることを意味しています。\(a\) には正の数字が入ります。この項は、正の値になるので、被食者の数が増えていくことを表現しています。例えば、新しいうさぎ(被食者)が生まれて増えるイメージです。
二番目の項にある "\(bxy\)" は、被食者の数と捕食者の数をかけて、\(b\) 倍していることを意味しています。\(b\) には正の数字が入ります。この項は、マイナスをかけて負の値になるので、被食者の数が減っていくことを表現しています。例えば、トラ(捕食者)が多ければ、うさぎ(被食者)が捕まって減ってしまうし、また、うさぎが多ければ、トラに捕まって減ってしまうイメージです。
✔︎ 正の数字を入れる \(a\) や \(b\) について
例えば、うさぎ(被食者)が100匹、トラ(捕食者)が10匹いるとすると、この微分方程式の右辺は \(100a - 1000b\) と表すことができます。
もし、\(a = 10, b = 1\) という数字が入れば、\(100a - 1000b = 0\) となるので、>被食者の数の時間変化がゼロとなり、被食者の数は将来に変化しないということになります。
つまり、方程式から導き出される結論は、被食者や捕食者の数はもちろんですが、(パラメータと言われる) \(a\) や \(b\) の値で変わってきます。
※ 次にでてくる \(c\) や \(d\) についても同じことが言えます。
次に、捕食者の数の時間変化は時間微分 \(\frac{dy}{dt}\) になるので、以下のような式を立てます。
$$\frac{dy}{dt} = cxy - dy$$
右の辺の最初の項にある "\(cxy\)" は、被食者の数と捕食者の数をかけて、 \(c\) 倍していることを意味しています。\(c\) には正の数字が入ります。この項は、正の値になるので、捕食者の数が増えていくことを表現しています。例えば、新しいトラ(捕食者)が生まれたり、うさぎ(被食者)が多ければトラが増えていくイメージです。
二番目の項にある "\(dy\)" は、捕食者の数を \(d\) 倍していることを意味しています。\(d\) には正の数字が入ります。この項は、マイナスをかけて負の値になるので、捕食者の数が減っていくことを表現しています。例えば、うさぎがいなくなってトラ(捕食者)が飢死していくようなイメージです。
Rをつかって、微分方程式モデルのシミュレーションをする
無料で使える統計解析ソフトウェアのRは、微分方程式モデルのシミュレーションにも使うことができます(Rについての詳細はこちらの記事をご参照ください)。
ここでは、"deSolve" パッケージを使用するので、以下のようにインストールして使える状態にします。
> install.packages("deSolve")
> library(deSolve)シミュレーションするためには、以下のようなスクリプトを実行します。
#モデルのパラメータを適当に設定
parameters <- c(a = 0.2, b = 0.7, c = 0.3, d = 0.5)
#被食者Xと捕食者Yに対して最初に割り振る数を設定(初期値の設定)
initial <- c(x = 100, y = 10)
#時間点を指定(ここでは、0, 0.01, 0.02, 0.03, ..., 2、に指定しています)
times <- seq(0, 2, 0.01)
#数理モデルの定義
LV_model <- function(t, state, parameters) {
with(as.list(c(state, parameters)), {
dx <- a * x - b * x * y #被食者の式に対応
dy <- c * x * y - d * y #捕食者の式に対応
list(c(dx, dy))
})
}
#ODE(Ordinary Differential Equation)関数を使って計算
out <- ode(y = initial, times = times, func = LV_model, parms = parameters)
計算が終わると、計算結果が "out" という変数に保存されています。
> head(out)
time x y
[1,] 0.00 100.00000 10.00000
[2,] 0.01 92.39431 13.28421
[3,] 0.02 83.23693 17.20819
[4,] 0.03 72.81687 21.64393
[5,] 0.04 61.68446 26.35269
[6,] 0.05 50.55652 31.02635計算によって得られた結果をプロットするには、例えば、以下のように実行します。
> matplot(out[,1], out[,2:3], type="l", xlim=c(0,2), col = c("black", "red"))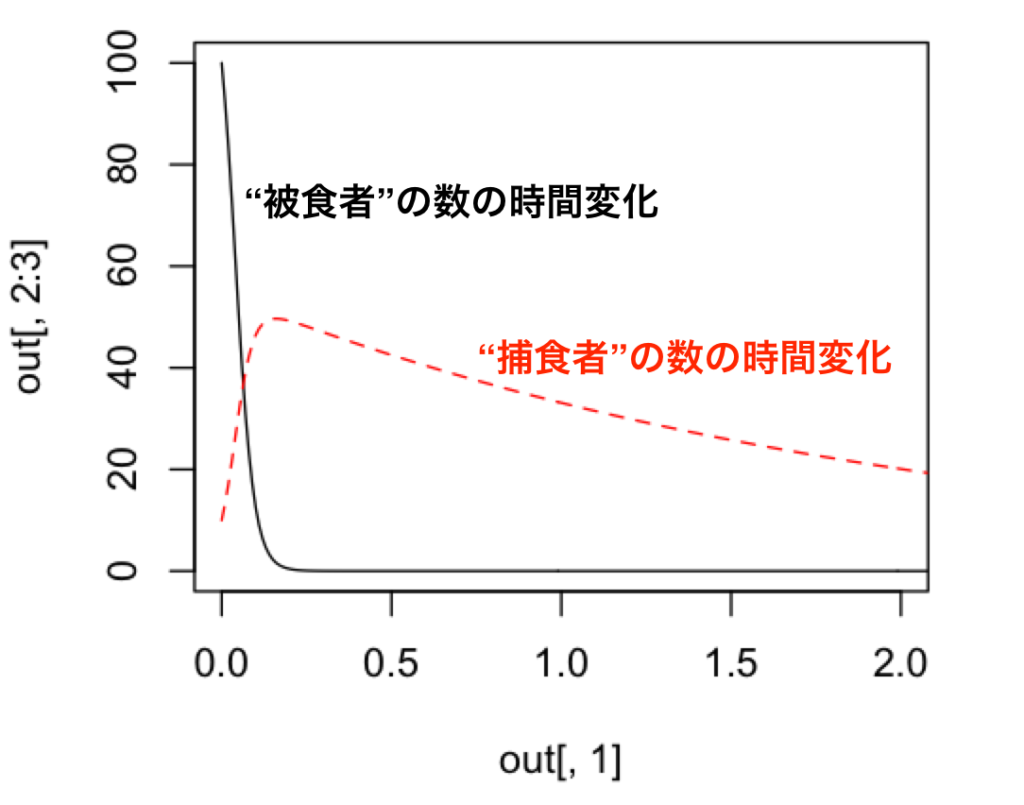
この図から、100匹いた被食者(うさぎ)が急激に減って、10匹いた捕食者(トラ)が急激に増えている様子がわかります。
ただし、被食者がゼロに近づくと、捕食者も減っていくことがわかります。
これらの結果は、"a" や "b"、"c"、"d" の値によって変わってくるので、いろいろな値で試してみてください。
関連記事
今回の記事では、「食べる者」と「食べられる者」の数の変化を表現する方程式である「ロトカ・ヴォルテラの方程式」を紹介しました。よく似た方程式に「ロトカ・ヴォルテラの競争方程式」もあって、同じ食糧を奪い合うような者同士の数の変化を表現するときに使えます。

