目次(まとめ)
◾️ 標準正規分布の上側確率は、上側パーセント点から得られる指標
◾️ 上側確率とパーセント点の関係は、正規分布表から調べることができる
◾️ 参考文献
◾️ 関連記事
こんにちは、みっちゃんです。
今回の記事では、統計で行う "仮説検定" や "信頼区間" を考えるときに不可欠な、標準正規分布の "上側確率" の意味と、それを得るための方法を紹介します。
標準正規分布の上側確率は、上側パーセント点から得られる指標
統計では、さまざまな確率分布が登場します(詳しくはこちらの記事をご覧ください)が、その基本となる分布が「標準正規分布」です。
標準正規分布において、上側パーセント点とは、標準正規分布にしたがう確率変数 \(X\) が、ある値 \(x\) 以上となる確率(上側確率)がそのパーセントに一致するときに、その値 \(x\) のことを意味します。
例えば、以下のような標準正規分布を考えます。
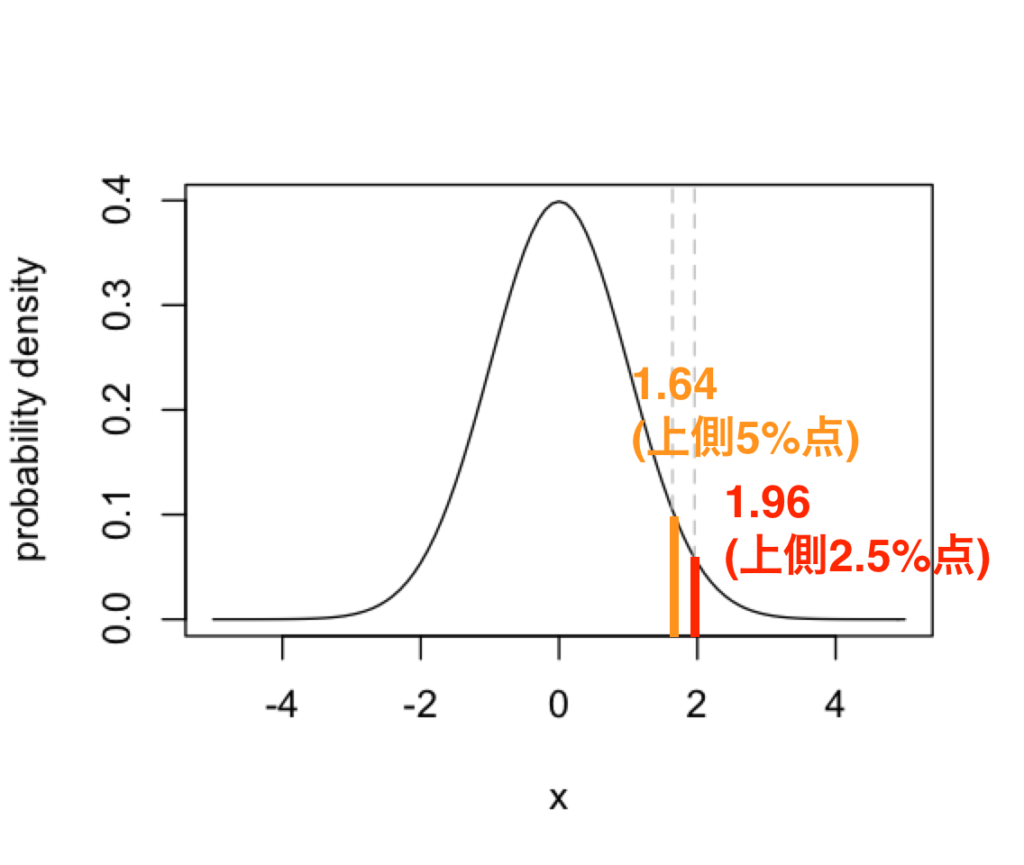
統計の分野でよく用いられるのが、「上側2.5パーセント点」と「上側5パーセント点」です。
「上側2.5パーセント点」が意味するのは、標準正規分布の上側確率が0.025になる \(x\) のことであり、その値は1.96になります。
また、「上側5パーセント点」が意味するのは、標準正規分布の上側確率が0.05になる \(x\) のことであり、その値は約1.64になります。
上側確率とパーセント点の関係は、正規分布表から調べることができる
統計の教科書をみると、よく巻末に「標準正規分布表」が掲載されています。
重要な箇所だけ抜き出すと、以下のようになっています。

緑の場所に示されている数値は「標準正規分布の横軸の座標」に相当し、青の場所に示されている数値は「上側確率」に相当します。
例えば、\(x = 1.96\) がわかっていて、それに相当する上側確率を考える場合には、図の赤矢印で示しているように見ることで、上側確率が0.025になることがわかります。
矢印を逆にたどれば、例えば、上側確率が0.025になるような \(x\) を見つけることもできます。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

