目次(まとめ)
◾️ 対数正規分布の確率密度関数と平均、分散
◾️ 対数正規分布のパラメータが確率分布に及ぼす効果
◾️ 対数を用いた変数変換を行うと正規分布になる
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、名前の通り「正規分布」と関連が深い「対数正規分布」について解説します。
対数正規分布の確率密度関数と平均、分散
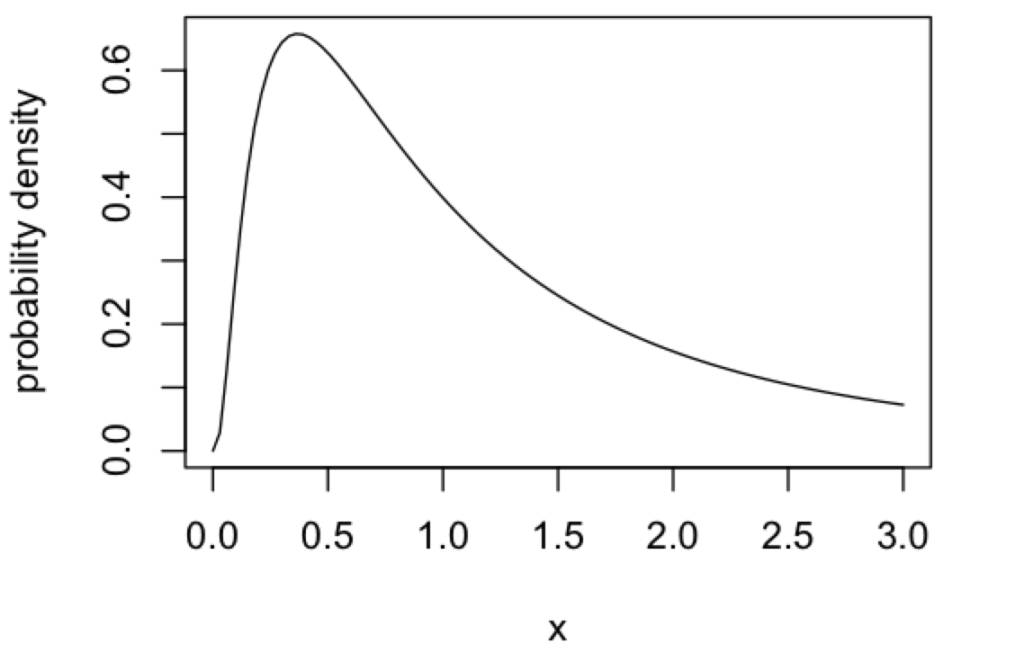
対数正規分布は、\(\mu\) (実数)と \(\sigma^2\)(正の定数)という2つのパラメータをつかって表現されます。
ちなみに、上の図で示している対数正規分布の確率密度関数は、以下のようにRで実行することで得られます(\(\mu = 0, \sigma^2 = 1\))(平均と “標準偏差” を指定しているので注意)。
> curve(dlnorm(x, 0, 1), xlab = "x", ylab = "probability density", xlim = c(0, 3))
対数正規分布の確率密度関数、平均、分散は、以下のように得られます。
確率密度関数
$$f_X(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \frac{1}{x} {\rm exp} \{-\frac{({\rm log} x - \mu)^2}{2 \sigma^2}\}$$
平均
$$E[X] = {\rm exp}\{\mu + \frac{\sigma^2}{2}\}$$
分散
$${\rm Var}(X) ={\rm exp}\{2(\mu + \sigma^2)\} - {\rm exp}\{2\mu + \sigma^2\}$$
対数正規分布のパラメータが確率分布に及ぼす効果
対数正規分布には、\(\mu\) と \(\sigma^2\) という2つのパラメータがあります。
まず、\(\sigma^2 = 1\) に固定して \(\mu\) を変化させてみます。
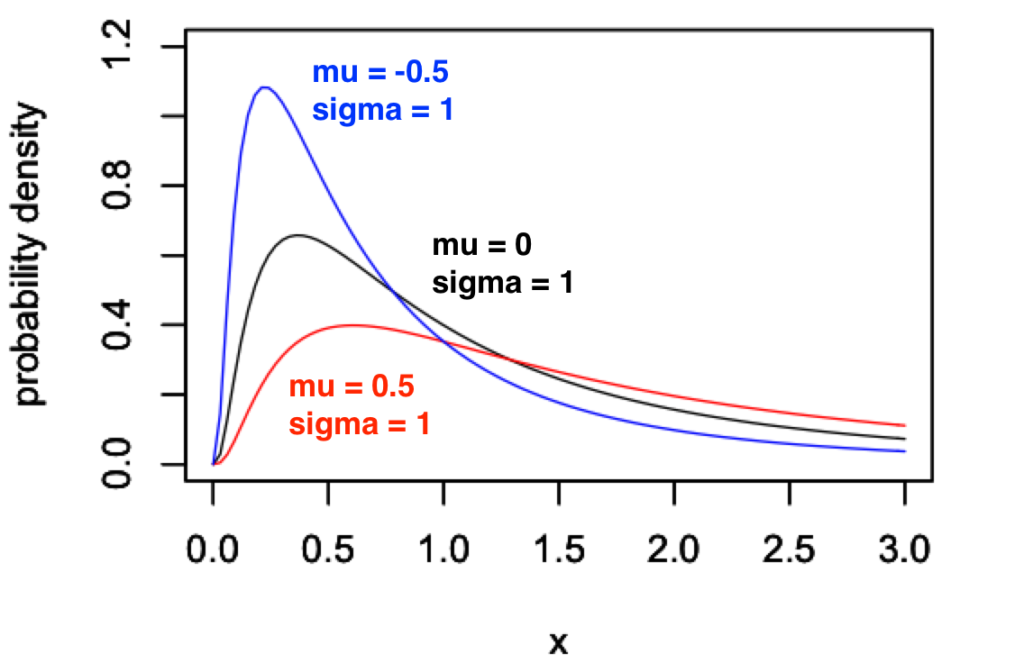
この図から、\(\mu\) の値を大きくしていくと、横広の分布になることがわかります。
次に、\(\mu = 0\) に固定して、\(\sigma\) を変化させてみます。
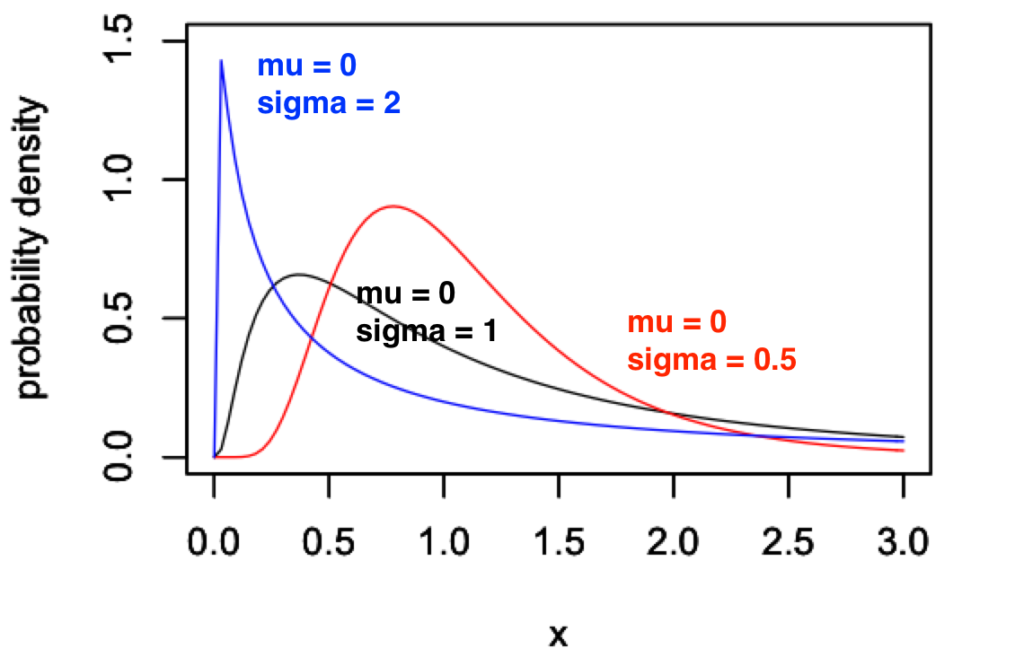
この図から、\(\sigma\) を大きくしていくと、分布が右の方に移動して、山も大きく変わっていくことがわかります。
対数を用いた変数変換を行うと正規分布になる
ここでは、\(Y = {\rm log}X = g(X)\) という変数変換を考えます。
この関係から、\(X = {\rm exp}\{Y\} = g^{-1}(Y)\) という関係が得られます。
公式から、\(Y\)の確率密度関数は次のように与えられます。
$$f_Y(y) = f_X(g^{-1}(y))|\frac{{\rm d}}{{\rm d}y} g^{-1}(y)|$$
したがって、対数正規分布の確率密度関数 \(f_X(x | \mu, \sigma^2)\) について、変数変換を行うと、以下のように正規分布の確率密度関数が得られます。
$$f_Y(y | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \frac{1}{{\rm exp}\{y\}} {\rm exp} \{-\frac{({\rm log} \{{\rm exp}\{y\}\} - \mu)^2}{2 \sigma^2}\} {\rm exp}\{y\}$$
$$ = \frac{1}{\sqrt{2\pi\sigma^2}} {\rm exp} \{-\frac{(y - \mu)^2}{2 \sigma^2}\}$$
参考文献
久保川達也「現代数理統計学の基礎」共立出版

