目次(まとめ)
◾️ ロジスティック分布の確率密度関数と平均、分散
◾️ ロジスティック分布のパラメータが確率分布に及ぼす効果
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、正規分布のように左右対称の確率変数の分布である「ロジスティック分布」について解説します。
ロジスティック分布の確率密度関数と平均、分散
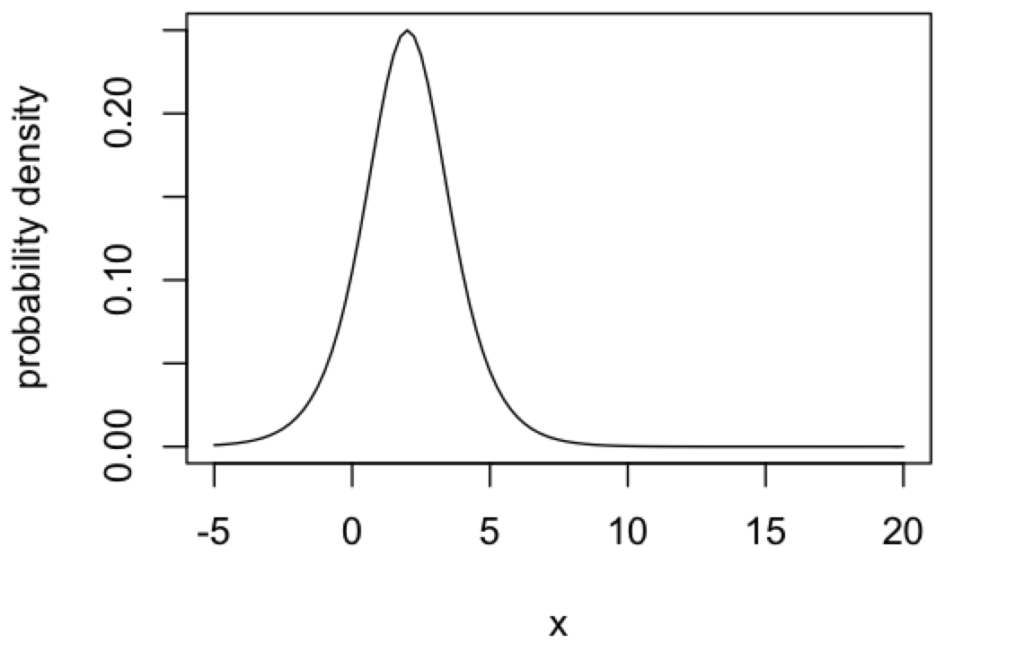
ロジスティック分布は、位置 \(\mu\) と尺度 \(\sigma\)という2つのパラメータをつかって表現されます。
ちなみに、上の図で示しているロジスティック分布の確率密度関数は、以下のようにRで実行することで得られます(\(\mu = 2, \sigma = 1\))。
> curve(dlogis(x, 2, 1), xlab = "x", ylab = "probability density", xlim = c(-5, 20))
ロジスティック分布の確率密度関数、平均、分散は、以下のように得られます。
確率密度関数
$$f_X(x | \mu, \sigma) = \frac{1}{\sigma(1 + {\rm exp} \{-\frac{x-\mu}{\sigma}\})^2} {\rm exp} \{-\frac{x-\mu}{\sigma}\}$$
平均
$$E[X] = \mu$$
分散
$${\rm Var}(X) = \frac{\pi^2\sigma^2}{3}$$
ロジスティック分布のパラメータが確率分布に及ぼす効果
ロジスティック分布には、位置 \(\mu\) と尺度 \(\sigma\) という2つのパラメータがあります。
まず、\(\sigma = 1\) に固定して \(\mu\) を変化させてみます。
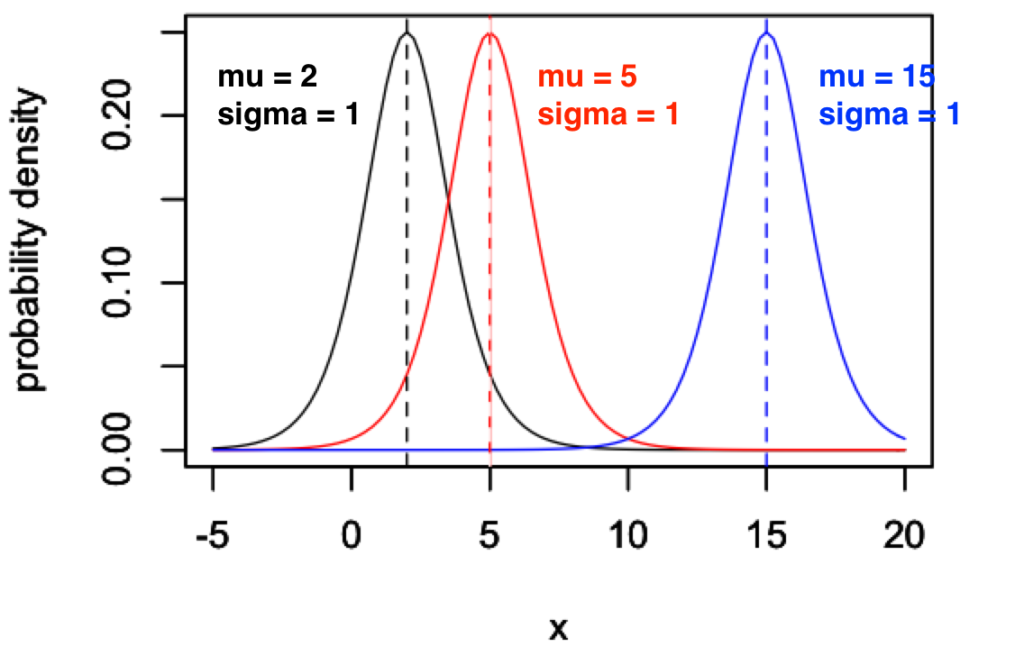
ロジスティック分布の平均が \(\mu\) であることからもわかりますが、\(\mu\) を変化させていくと、分布が \(\mu\) で左右対称になるように、平行移動していきます。
次に、\(\mu = 2\) に固定して、\(\sigma\) を変化させてみます。
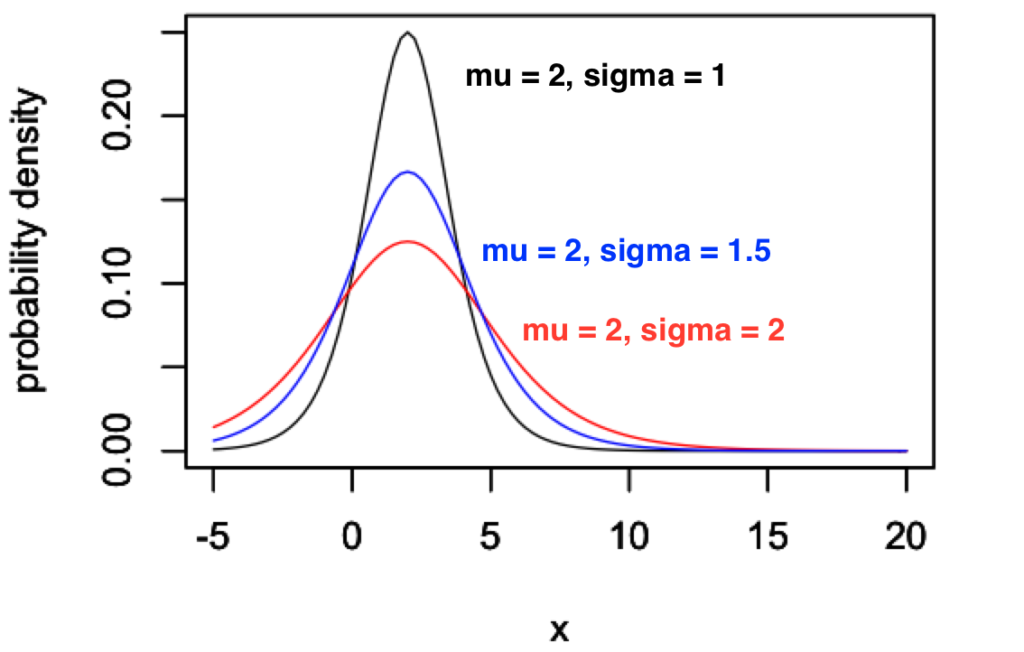
この図から、\(\sigma\) の値が小さいときは尖った曲線になり、\(\sigma\) を大きくしていくと、尖りがなくなり横広の曲線に変わっていくことがわかります。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

