目次(まとめ)
◾️ 幾何分布の確率関数、確率母関数、平均、分散
◾️ 2項分布、幾何分布、負の2項分布などベルヌーイ試行に関係する分布の違い
◾️ 幾何分布が無記憶性をもつことを証明する
◾️ 参考文献
こんにちは、みっちゃんです。
以前の記事で、ベルヌーイ試行で得られた結果について、全体の中で成功した回数の分布を考える「2項分布」について紹介しました。
今回の記事では、2項分布と同様にベルヌーイ試行で得られた結果についての確率分布である「幾何分布」について解説します。
幾何分布の確率関数、確率母関数、平均、分散
幾何分布は、ベルヌーイ試行にしたがう分布であり、初めて成功するまでの失敗の回数についての分布です。
離散分布なので、確率密度関数ではなく、確率関数が定義されます。
確率関数
$$P(Y = k | p) = p (1-p)^k \qquad (k = 0, 1, 2, …)$$
幾何分布の平均は \( \frac{1-p}{p}\)、分散は \(\frac{1-p}{p^2}\) になります。
平均や分散は、以下の確率母関数を用いて取得することもできます(詳細はこちら、もしくは、こちらの記事をご覧ください)。
確率母関数
$$G_X(s) = \frac{p}{1-(1-p)s}$$
2項分布、幾何分布、負の2項分布などベルヌーイ試行に関係する分布の違い
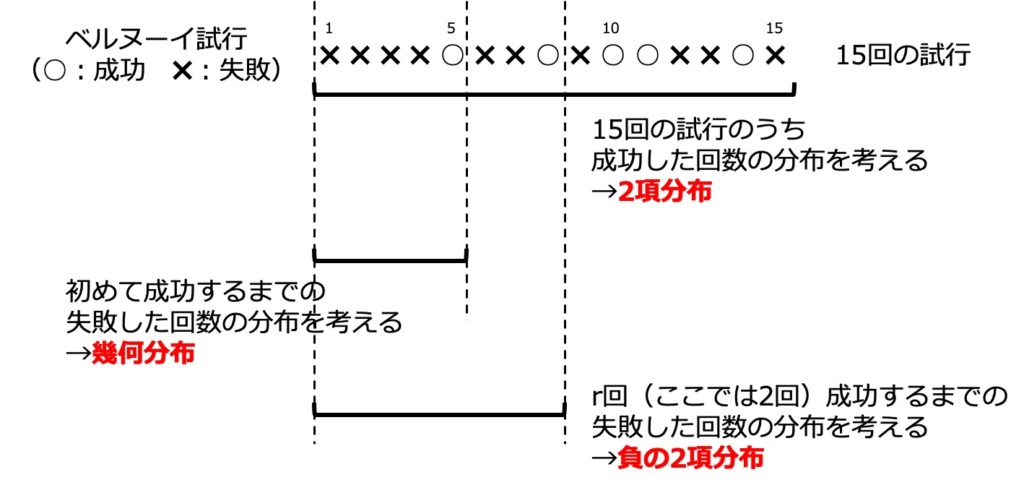
ベルヌーイ試行に関係する確率分布には、2項分布や幾何分布、負の2項分布などがあります。
これらの確率分布の違いは、ベルヌーイ試行で得られる結果について何に注目するか、という点にあります。
例えば、上で示すように、\(p\) の確率で「成功」、\(1-p\) の確率で「失敗」するようなベルヌーイ試行を15回繰り返すとき、全体の中で「成功」した回数の分布を考えるのが「2項分布」です(詳細はこちらの記事をご覧ください)。
「幾何分布」は、15回全体には興味がなく、初めて成功するまでに「失敗」した回数の分布を考えます。
「負の2項分布」は、複数回成功するまでに「失敗」した回数の分布を考えます。
幾何分布が無記憶性をもつことを証明する
上の図に示した例では「幾何分布」は、ベルヌーイ試行の5回目に「成功」するまでの「失敗」の分布を考えます。
幾何分布では、例えば、3回までの試行において「成功」していないという条件のもとで4回までの試行で「成功」しないという確率は、3回までの試行において「成功」していないという条件とは無関係になります。
より一般的に書くと、\(P(X \geq 3)\) という条件のもとで \(P(X \geq 3+1)\) を考えても、結局 \(P(X \geq 1)\) を考えるのと同じということです。
これを証明するためには、まず、\(P(X \geq 3)\) を計算する必要があります。
その際には、 \(P(X = 3), P(X = 4), ..., P(X = \infty)\) の確率を足し合わせます。
$$P(X \geq 3) = \sum_{k=3}^{\infty} p(1-p)^k$$
$$\qquad = p(1-p)^3 + p(1-p)^4 + p(1-p)^5 + ・・・$$
これは、初項 \(p(1-p)^3\)、公比 \((1-p)\) の等比数列なので、等比数列の和の公式から、以下のようになります。
$$P(X \geq 3) = \sum_{k=3}^{\infty} p(1-p)^k = \frac{p(1-p)^3}{p} = (1-p)^3$$
今考えているのは、\(P(X \geq 3 + 1 | X \geq 3)\) が \(P(X \geq 1)\) になるか、ということなので、式を変形していきます。
$$P(X \geq 3 + 1 | X \geq 3) = \frac{P(X \geq 3 + 1, X \geq 3)}{P(X \geq 3)}$$
$$\qquad = \frac{(1-p)^4}{(1-p)^3} = (1-p)^1 = P(X \geq 1)$$
したがって、幾何分布は、指数分布と同様に、無記憶性を持ち、「成功」という現象がランダムに起こるということになります。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

