目次(まとめ)
◾️ 2項分布はベルヌーイ試行に基づく分布
◾️ 2項分布の確率関数、確率母関数、積率母関数、特性関数、平均、分散
◾️ 参考文献
こんにちは、みっちゃんです。
前回の記事では、大量に観測されたデータの中で、珍しく発生する現象について、その数の分布を表す「ポアソン分布」について解説しました。
今回の記事では、「ポアソン分布」に近づく「2項分布」について解説します。
2項分布はベルヌーイ試行に基づく分布
ベルヌーイ試行とは、\(p\) の確率で「成功」、\(1-p\) の確率で「失敗」するような試行です。
例えば、表裏があるコインを投げるという試行(実験)を行うときに、「コインの表がでる」ということを「成功」とするというようなことです。
2項分布の確率関数、確率母関数、積率母関数、特性関数、平均、分散
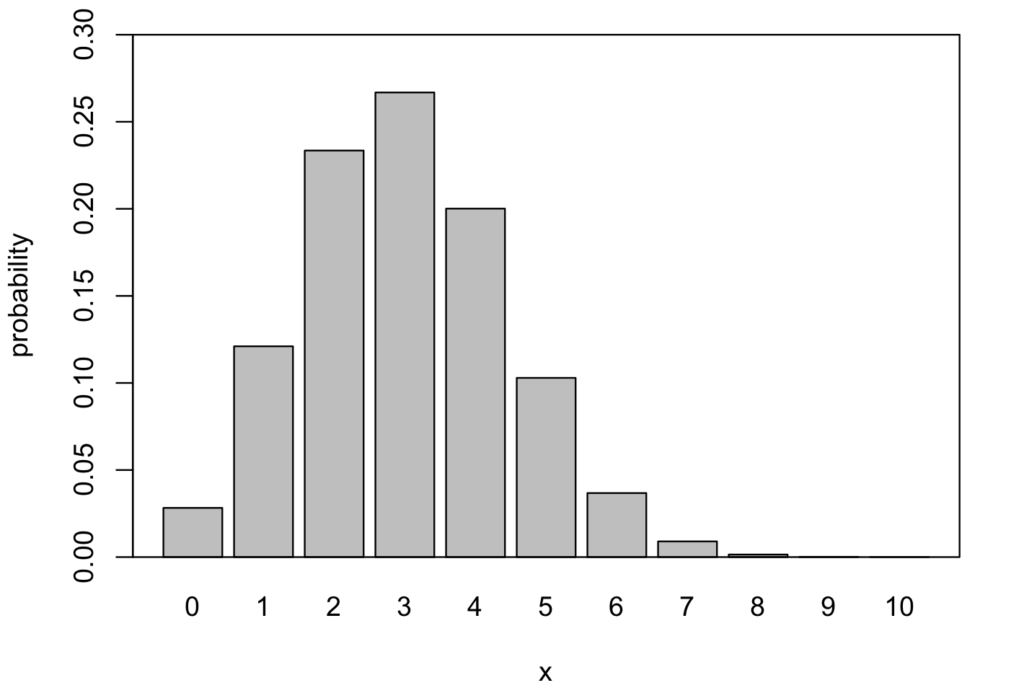
2項分布は、ベルヌーイ試行にしたがう分布であり、\(n\) 回の試行のうち \(p\) の確率で成功する、\(k\) 回の成功についての分布です。
離散分布なので、確率密度関数ではなく、確率関数が定義されます。
確率関数
$$P(Y = k | n, p) = {}_n \mathrm{C}_k p^k (1-p)^{n-k} \qquad (k = 0, 1, 2, …, n)$$
ちなみに、上の図で示している2項分布の確率関数は、以下のようにRで実行することで得られます(\(n = 10, p = 0.3\))。
> x <- 0:10
> barplot(dbinom(x, 10, 0.3), ylim = c(0, 0.3), names = c(0:10), xlab = "x", ylab = "probability")
> box()2項分布の平均は \( np\)、分散は \(np(1-p)\) になります。
平均や分散は、以下の確率母関数や積率母関数、特性関数を用いて取得することもできます(詳細はこちら、もしくは、こちらの記事をご覧ください)。
確率母関数
$$G_X(s) = (ps + 1 - p)^n$$
積率母関数
$$M_X(t) = (pe^t + 1 - p)^n$$
特性関数
$$\varphi_X(t) = (pe^{it} + 1 - p)^n$$
参考文献
久保川達也「現代数理統計学の基礎」共立出版

