目次(まとめ)
- k最近傍法は、最近傍法(k=1)を拡張した手法
- 近傍にあるk個のデータのクラスを見て、多いクラスに割り当てる
- 参考文献
こんにちは、みっちゃんです。
今回の記事では「手元にあるデータをクラス分けして、新しいデータに対して適切なクラスを見つけたい」という方向けに「k最近傍法(kNN法)」を紹介します。
k最近傍法は、最近傍法(k=1)を拡張した手法
以前の記事で「ボロノイ図」について紹介しました。
ボロノイ図は、手持ちのデータの特徴と新たなデータの特徴を比較して、新たなデータに一番似ている手持ちのデータを視覚的に探索するときに便利です。
この図は「最近傍法」のデータ探索手順を可視化しているものです。
図の中で最も近傍にある点、つまり、一番似ているデータを探索するアプローチです。
今回の記事で紹介する「k最近傍法」は、最も近傍にあるデータだけではなく、近傍にあるk個のデータに注目して、データのクラス分けをするための手法です。
近傍にあるk個のデータのクラスを見て、多いクラスに割り当てる
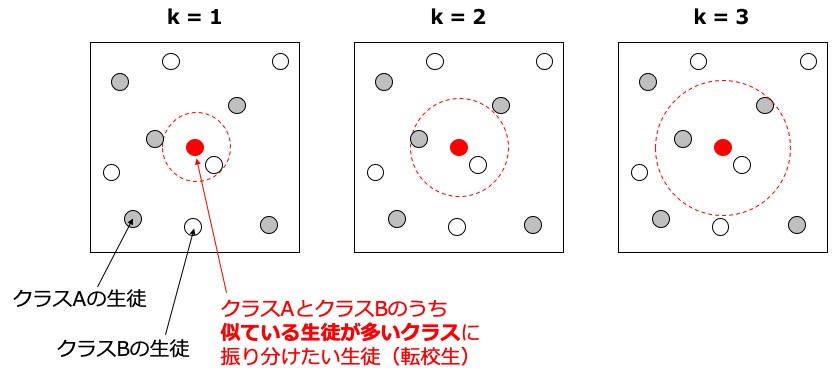
上に示している図は、クラスAに所属している生徒5人、クラスBに所属している生徒5人の算数と国語の点数の散布図と思ってください(例えば、以前の記事と同じように、横軸が算数の点数、縦軸が国語の点数を表しているとします)。
いまやりたいことは、赤で示している転校生を、算数と国語の点数に注目して、クラス分け、つまり、クラスAかクラスBに振り分けることです。
「k最近傍法」では、以下のようにクラス分けを行います。
k = 1のとき(左図)
転校生の点数から一番近い生徒が所属するクラスに振り分けます。したがって、転校生はクラスBになります。
k = 2のとき(中図)
転校生の点数から近い生徒を2人選び、その生徒が所属するクラスに振り分けます。この場合、1人はクラスA、もう1人はクラスBなので、転校生を振り分けることはできません。
k = 3のとき(右図)
転校生の点数から近い生徒を3人選び、その生徒が所属するクラスに振り分けます。3人のうち2人がクラスAに所属しているので、多数決で、転校生はクラスAになります。
このように、kを変えていくと、振り分けるべきクラスが変わっていくことがわかります。また、場合によっては、振り分けるべきクラスを決定することができない状況が生じます(今回の例では、k = 2のとき)。したがって、kの値を変えながら、適切なクラス分けを調べる必要があります。

