目次(まとめ)
- 次元圧縮とは「高い次元」で表現されたデータを「低い次元」で表現すること
- 次元圧縮法として「主成分分析」や「t-SNE」が知られている
- 次元圧縮の結果をSleepwalkを用いて比較する
- 参考文献
こんにちは、みっちゃんです。
今回の記事では「複数の次元圧縮の方法があるけれども、その圧縮結果の違いを可視化して比較したい」という方向けに、Sleepwalkというツールを紹介したいと思います。
次元圧縮とは「高い次元」で表現されたデータを「低い次元」で表現すること
ここでは、説明のために、Rにあらかじめ準備されている車の性能データ(mtcars)を使用します。
したがって、手持ちのファイルから読み込みを行う必要がありません。
以下のように実行することで、"mtcars" の一部を取り出して、データの外観を知ることができます。
> head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1ここでは便宜上、"mtcars" のスケールのばらつきを解消するため、以下のように実行して、"data" という変数に "mtcars" を読み込みます。
> data <- scale(mtcars)データは、以下のようになっています。
> head(data)
mpg cyl disp hp drat
Mazda RX4 0.1508848 -0.1049878 -0.57061982 -0.5350928 0.5675137
Mazda RX4 Wag 0.1508848 -0.1049878 -0.57061982 -0.5350928 0.5675137
Datsun 710 0.4495434 -1.2248578 -0.99018209 -0.7830405 0.4739996
Hornet 4 Drive 0.2172534 -0.1049878 0.22009369 -0.5350928 -0.9661175
Hornet Sportabout -0.2307345 1.0148821 1.04308123 0.4129422 -0.8351978
Valiant -0.3302874 -0.1049878 -0.04616698 -0.6080186 -1.5646078
:
このように、"data" は、さまざまな車の性能(例えば、mpg, cyl, dispなど)を示すデータになっています。
しかしながら、性能の種類が多いため、どの車とどの車が性能的に似ている車なのか判断することができません。
次元圧縮の手法は、一般的に、"data" のように、高次元の項目からなるデータを、2次元のプロットで可視化します。
次元圧縮法として「主成分分析」や「t-SNE」が知られている
次元圧縮および可視化は、さまざまなプログラミング言語で行うことができます。
以前の記事では、Pythonというプログラミング言語を使った主成分分析について紹介しました。
Rで「主成分分析」を行うためには、以下のように実行します。
> data.pca <- prcomp(data)上のように実行して主成分分析を行うと、"data.pca" の中には、さまざまな変数が出来上がります。
一般に、"data.pca" の中の変数のうち、「主成分スコア」に相当する "data.pca$x" に注目し、その1列目のデータ(PC1)と2列目のデータ(PC2)を可視化に用います。
ここでは、説明のため、"data.pca$x" の1列目、2列目のデータを、"pca_score" という変数に入れます。
> pca_score <- data.pca$x[,1:2]> head(pca_score)
PC1 PC2
Mazda RX4 -0.64686274 1.7081142
Mazda RX4 Wag -0.61948315 1.5256219
Datsun 710 -2.73562427 -0.1441501
Hornet 4 Drive -0.30686063 -2.3258038
Hornet Sportabout 1.94339268 -0.7425211
Valiant -0.05525342 -2.7421229
可視化をするためには、以下のように実行します。
> plot(pca_score[,1], pca_score[,2])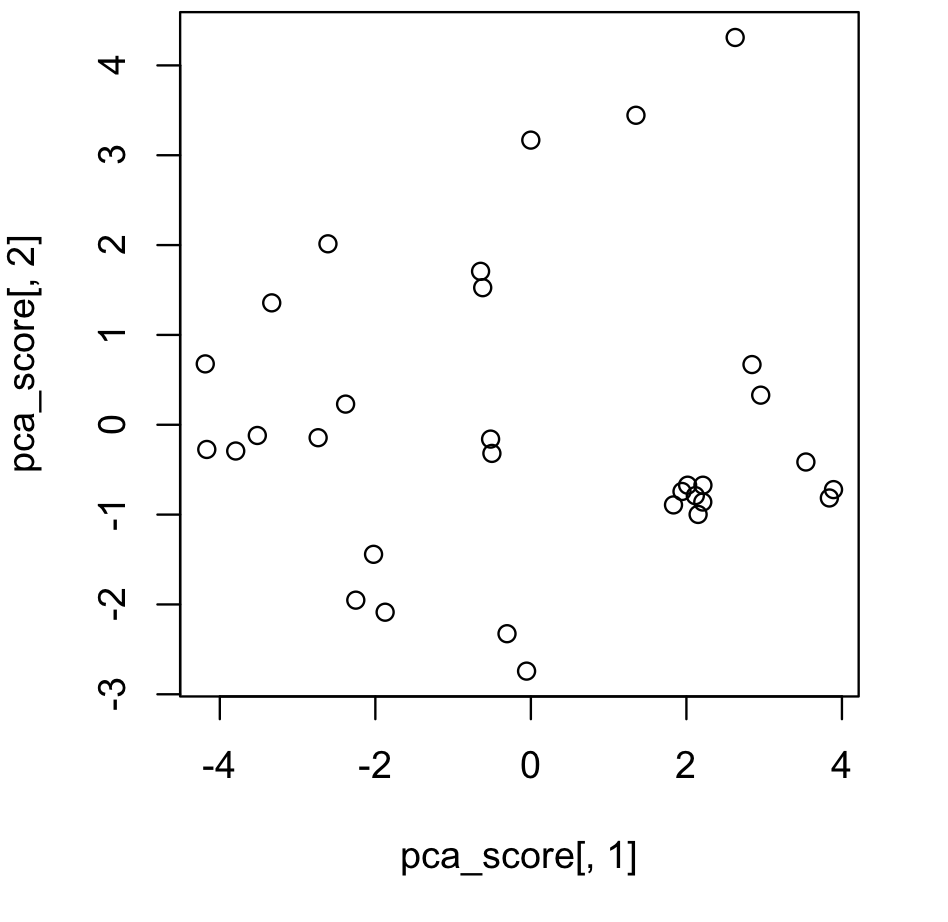
寄与率は、以下のように算出することができます。
> summary(data.pca)$importance[,1:2]一方で、Rで「t-SNE」を行うためには、以下のように実行します。
## インストールしていなければ実行する箇所 ##
## > install.packages("tsne")
## > library(tsne)
> tsne_score <- tsne(data)> head(tsne_score)
[,1] [,2]
[1,] -519.21880 -727.9274
[2,] -804.82308 -344.7616
[3,] 84.40050 635.6234
[4,] 1042.94455 -716.2675
[5,] 796.42922 154.5143
[6,] 74.28509 1520.8283可視化をするためには、以下のように実行します。
> plot(tsne_score[,1], tsne_score[,2])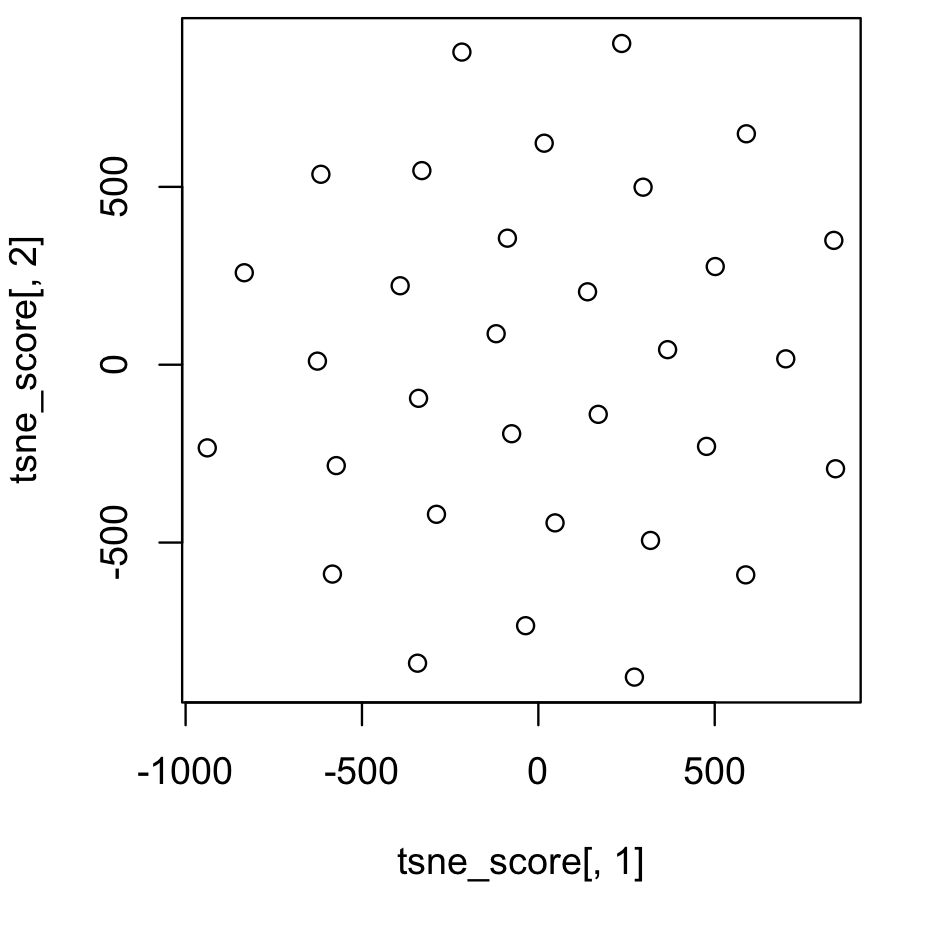
次元圧縮の結果をSleepwalkを用いて比較する
上に示した結果からもわかるように、次元圧縮をする手法はさまざまです。
また、得られる結果もさまざまです。
そこで、Sleepwalkというツールを用いて、可視化の結果を比較することが有用です。
実行方法は、以下の通りです。
## インストールしていなければ実行する箇所 ##
## > install.packages("sleepwalk")
## > library(sleepwalk)
> sleepwalk(list(pca_score, tsne_score), list(data, data), point = 5)基本的には「sleepwalk(A, B)」という形式で、AとBという2つの行列を設定します。
Aは次元圧縮法で得られたもので可視化したいもの、Bは次元圧縮法を実行したもとのデータです。
ここでは、Aには、"pca_score" と "tsne_score" という2つの行列を設定したいので、listとして2つ並べています。
それに応じて、Bもlistとして2つ並べています。
※3つ以上の比較を行いたい場合にも、同じような形式で実行すれば、可視化することが可能です。
また、"point" は、プロットサイズを変更するためのオプションです。
これを実行すると、ブラウザが自動的に開き、以下のように表示されます。
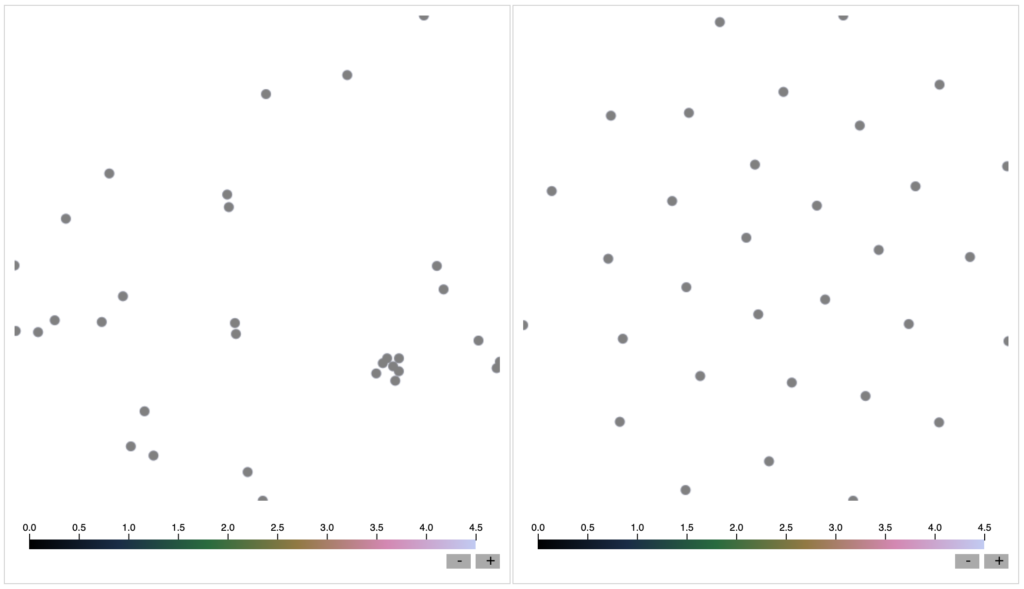
左側が「主成分分析」による結果、右側が「t-SNE」の結果です。
この図は、インターラクティブであり、片方の図にマウスを点に合わせると、もう片方の図に対応する点が表示されます。
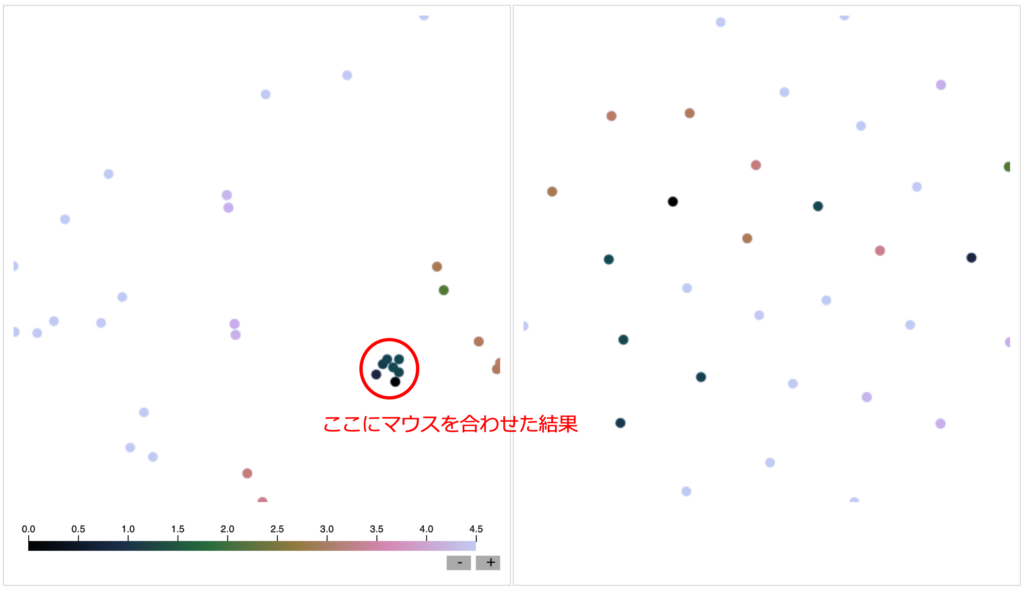
例えば、左の「主成分分析」の結果について、赤色で示した場所にマウスを合わせると、上のように表示されます。
下に示されているカラーバーが意味するのは、マウスを置いている点からの距離で、距離が近いほど小さい値に対応しています。
ここで、距離というのは、その点と点が表すデータがどれだけ似ているということを示しています。
濃い色は似ている、薄い色は似ていないことを示しています。
試してみるとわかると思いますが、「主成分分析」ではマウスを置いた点の周りが濃くなりますが、「t-SNE」ではそうはなりません。
つまり、「主成分分析」は似ているデータが近くになるような次元圧縮法ですが、「t-SNE」では必ずしもそうはならないということを意味しています。
みなさんも手持ちのデータで試してみてください。
参考文献
S. Ovchinnikova and S. Anders: Exploring dimension-reduced embeddings with Sleepwalk. BioRvix 603589 (2019). doi:10.1101/603589.

