この記事では、機械学習入門シリーズとして、サポートベクトルマシンを簡単に紹介したいと思います。
目次(まとめ)
◾️ サポートベクトルマシンとは、異なるグループのデータを判別する機械学習モデルの1つ
◾️最適な判別モデルは、異なるグループのデータができるだけ離れるようにする
◾️距離を最大化する最適化法はさまざま存在する
◾️ 参考文献
サポートベクトルマシンとは異なるグループのデータを判別する機械学習モデルの1つ
機械学習の分野では、歴史的に、3品種(setosa、versicolor、virginica)のアヤメの観測データ(花弁の長さ、花弁の幅、ガクの長さ、ガクの幅)が用いられてきたので、ここでもアヤメを例にあげて説明したいと思います。
サポートベクトルマシンは、2群データを判別するための技術、つまり、「setosa種のアヤメ」か、「setosa以外の種のアヤメ」を判別するための技術です。判別するためのデータとして、花弁やガクについての観測データを用いることになります。例えば(花弁の長さ:2cm、花弁の幅:1cm、ガクの長さ:3cm、ガクの幅:2cm)のアヤメなら、「setosa種のアヤメ」だと判別するといった感じです(←値は適当です)。
少し数式を取り扱いたいので、花弁の長さ:\(x_1\)、花弁の幅:\(x_2\)、ガクの長さ:\(x_3\)、ガクの幅:\(x_4\)とします。サポートベクトルマシンを用いて、「setosa種のアヤメ」か、「setosa以外の種のアヤメ」を判別するため、1つ1つのアヤメに対して以下のような式を設定します。
$$w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + b = {\bf w}^T{\bf x} + b$$
サポートベクトルマシンの目的は、図1に示すように、\({\bf w}^T{\bf x} + b = 0\)となる分離超平面を設計・構築することです。つまり、「setosa種のアヤメ」であれば\({\bf w}^T{\bf x} + b > 0\)、「setosa以外の種のアヤメ」であれば\({\bf w}^T{\bf x} + b < 0\)となるように、係数ベクトル\({\bf w}\)と切片\(b\)を調整していきます。
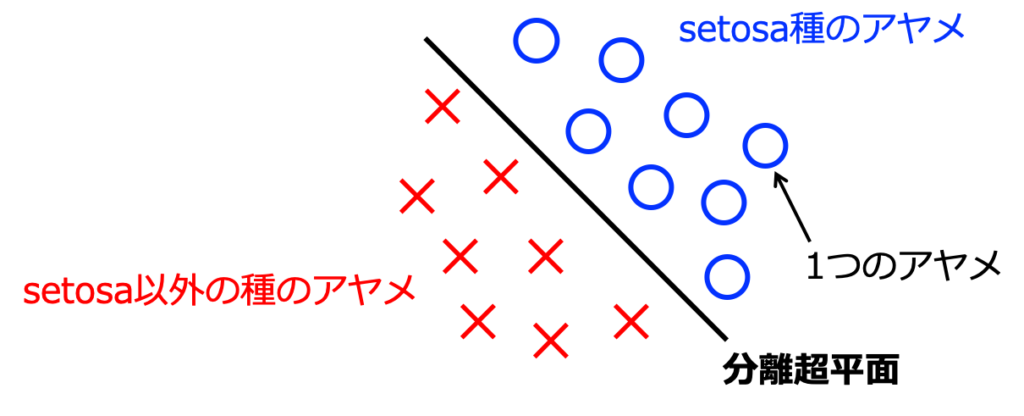
最適な判別モデルは、異なるグループのデータができるだけ離れるようにする
図1では、分離超平面を1つだけしか示していませんが、無限に描くことが可能です。したがって、ただ"判別"するということであれば、係数ベクトル\({\bf w}\)と切片\(b\)の調整は簡単です。サポートベクトルマシンでは、無限に存在する分離超平面の中から、もっとも全体をきれいに判別する超平面を選択することを目指します。ここで、サポートベクトルマシンの名前の由来にもなっている"サポートベクトル"が用いられます。
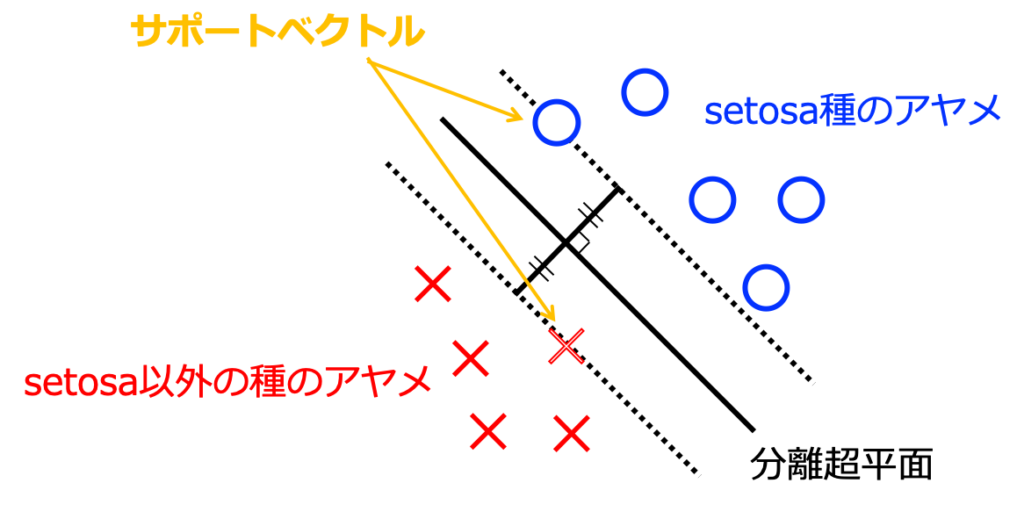
一般に、分離超平面からそれぞれのデータ(アヤメ)までの距離(マージン)は、\(||{\bf w}|| = \sqrt{{w_1}^2 + {w_2}^2 + \cdots}\)(2乗根に囲まれているので\(l_2\)ノルムと呼ばれます)を用いて以下のように表現されます。
$$d = \frac{|{\bf w}^T{\bf x} + b|}{||{\bf w}||}$$
以上のことから、サポートベクトルマシンで解くべき問題は、以下のように表現されます。
$$\underset{w, b}{{\rm max}},d$$
このときに満たすべき条件は、すべてのデータ(\(i = 1, 2, ..., n\))に対して、以下の不等式を満たすことである。
$$\frac{y_i({\bf w}^T{\bf x}_i + b)}{||{\bf w}||}\geq d$$
ここで、\(y_i\)はデータが属する群を+1, -1で表現するためのラベル変数であり、今回の例では、「setosa種のアヤメ」であれば\(y_i = +1\)、「setosa以外の種のアヤメ」であれば\(y_i = -1\)となります。なぜなら、\({\bf w}^T{\bf x}_i + b\)の符号が、それぞれ+1, -1となっているためです(距離は負の値に対して定義できない)。
距離を最大化する最適化法はさまざま存在する
マージン(距離)を最大化するような解を数値的に求めることは難しいのですが、これまでにいくつかの手法が提案されています。
サポートベクトルマシンでは、ラグランジュ関数を導入して解を求めていくことが用いられているのですが、この詳細はややこしくなるので、以下の参考文献などをご参照ください。
参考文献
- 小西貞則「多変量解析入門」岩波書店
:文章での説明が充実していて、わかりやすいと思います。
- 平井有三「はじめてのパターン認識」森北出版

