目次(まとめ)
◾️ 連続一様分布の平均と分散
◾️ 確率変数 \(X\) の(累積)分布関数を考える
◾️ 新たな確率変数を定義して期待値を求める
こんにちは、みっちゃんです。
今回の記事では、2013年に行われた統計検定1級の統計数理の問題(問1)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
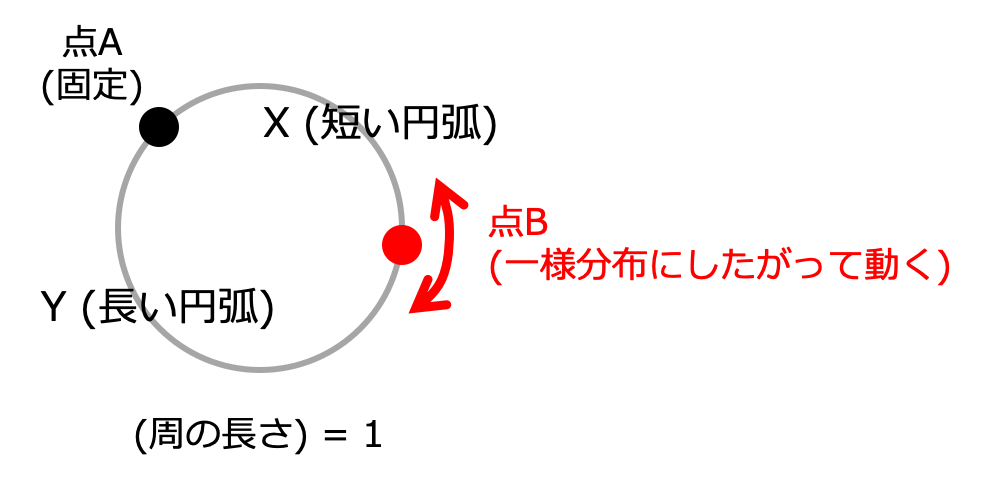
この問題では、以下の図で示すように、周の長さが1の円周上において、A点とB点がなす円弧の長さを確率変数 \(X\) と \(Y\) で表現しています。
連続一様分布の平均と分散
以前の記事で紹介したように、ある区間(閉区間)[a, b] において確率変数 \(X\) が連続一様分布を示す時、平均、分散は以下のように与えられます。
平均
$$E[X] = \frac{a + b}{2}$$
分散
$${\rm Var}(X) = \frac{(b - a)^2}{12}$$
この問題では、周の長さが1の円周の短い円弧を、確率変数 \(X\) と表現していることから、\(X\) は閉区間 [0, 0.5] の範囲で連続一様分布にしたがうことになります。
一方、円周の長い円弧を、確率変数 \(Y\) と表現していることから、\(Y\) は閉区間 [0.5, 1] の範囲で連続一様分布にしたがうことになります。
したがって、確率変数 \(X\) と \(Y\) の期待値は、以下のように得られます。
$$E[X] = \frac{0 + 0.5}{2} = 0.25E[Y] = \frac{0.5 + 1}{2} = 0.75$$
また、確率変数 \(X\) が大きくなると、確率変数 \(Y\) が小さくなるという関係があるので、両者の相関係数は \(-1\) となります。
確率変数 \(X\) の(累積)分布関数を考える
以前の記事で紹介したように、確率変数 \(X\) の(累積)分布関数 \(F_X (x)\) は以下のように与えられます。
$$F_X (x) = P(X leq x)$$
また、中学校などで習ったように、確率変数 \(X\) がとるすべての値を足し合わせると "1" になります。
この問題では、確率変数 \(X\) が取りうる値が [0, 0.5] なので、以下のような関係が成り立つことがわかります。
$$F_X (x) = P(X \leq x) = 2x$$
例えば、\(x = 0.5\) とすると \(F_X (0.5) = P(X \leq 0.5) = 1\) となります。
新たな確率変数を定義して期待値を求める
この問題では、新たな確率変数として \(W\) が、以下のように定義されています。
$$W = \frac{X}{1 - X}$$
この確率変数の(累積)分布関数は、\(P(X \leq x) = 2x\) であるため、以下のように求めることができます。
$$F_W (w) = P(W \leq w) = P(\frac{X}{1 - X} \leq w) = P(X \leq \frac{w}{w + 1}) = \frac{2w}{w + 1}$$
(累積)分布関数を微分し、確率密度関数を以下のように求めることができます。
$$f_W (w) = F_W' (w) = \frac{2}{(w + 1)^2}$$
確率変数 \(W\) の期待値は、以下のように求めることができます。
$$E[W] = \int_0^1 w f_W (w) dw = 2 {\rm log} 2 -1$$

