目次(まとめ)
◾️ 一様分布にしたがう確率変数の大小関係を考える
◾️ 参考文献
◾️ 関連記事
こんにちは、みっちゃんです。
今回の記事では、2012年に行われた統計検定1級の統計数理の問題(問1)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
この問題では、確率積分変換によって得られる区間(0,1)の一様分布が取り上げられています(確率積分変換についてはこちらの記事をご参照ください)。
一様分布にしたがう確率変数の大小関係を考える
この問題では、互いに独立に区間(0,1)上の一様分布にしたがう確率変数 \(U_1, U_2, U_3\) を考えます。
いま、これらの確率変数の中で、一番大きいもの、つまり、\({\rm max}(U_1, U_2, U_3)\) を \(X_3\) と置き、\(X_3\) の確率密度関数 \(g_3(x)\) を求めることを考えます。
確率密度関数は、累積分布関数を微分したものに相当する、つまり、
$$g_3(x) = \frac{{\rm d}}{{\rm d}x} G_3(x)$$
なので、まず累積分布関数 \(G_3(x)\) を考えます。
累積分布関数の定義から、\(G_3(x) = {\rm Pr} (X_3 \leq x)\) となるので、
$$G_3(x) = {\rm Pr} (X_3 \leq x) = {\rm Pr} ({\rm max}(U_1, U_2, U_3) \leq x)$$
となるが、これは、3つの確率変数 \(U_1, U_2, U_3\) が、すべて \(x\) より小さくなる状況と同じになります。
つまり、
$$\begin{eqnarray}G_3(x) &=& {\rm Pr} ((U_1 \leq x) \cap (U_2 \leq x) \cap (U_3 \leq x))\\&=&{\rm Pr} (U_1 \leq x) \times {\rm Pr}(U_2 \leq x)\times {\rm Pr}(U_3 \leq x)\end{eqnarray}$$
となります。ここで、\({\rm Pr}(U_j \leq x) ~ (j = 1, 2, 3)\) は、確率変数 \(U_j\) の累積分布関数に相当し、その値は区間(0, 1)において \(x\) になります(つまり、確率密度関数が "1" になる)。
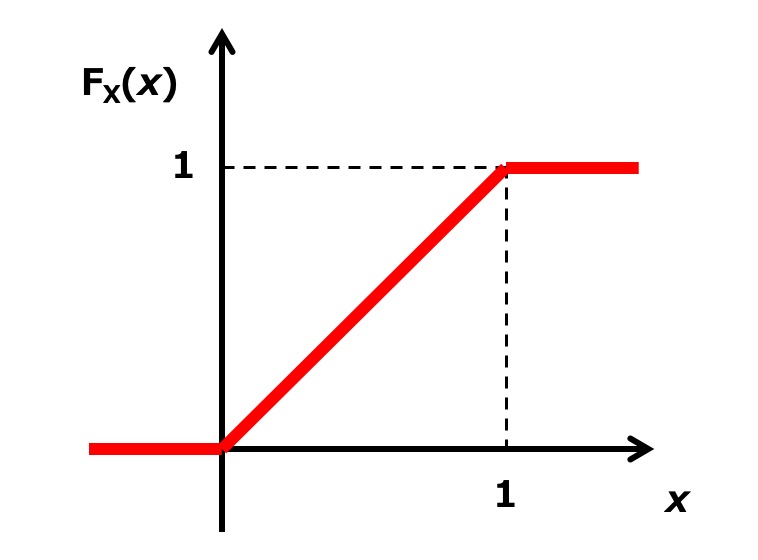
したがって、累積分布関数 \(G_3(x)\) は \(x^3\) となり、確率密度関数 \(g_3(x)\) は \(3x^2\) になります。
次に、確率変数 \(U_1, U_2, U_3\) の中で、一番小さいもの、つまり、\({\rm min}(U_1, U_2, U_3)\) を \(X_1\) と置き、\(X_1\) の確率密度関数 \(g_1(x)\) を求めることを考えます。
先ほどと同様に、累積分布関数から考えますが、その定義から、\(G_1(x) = {\rm Pr} (X_1 \leq x)\) となるので、
$$\begin{eqnarray}G_1(x) &=& {\rm Pr} (X_1 \leq x) \\&=& {\rm Pr} ({\rm min}(U_1, U_2, U_3) \leq x)\\&=& 1 - {\rm Pr} ({\rm min}(U_1, U_2, U_3) > x)\end{eqnarray}$$
となりますが、 \({\rm Pr} ({\rm min}(U_1, U_2, U_3) > x)\) は、3つの確率変数 \(U_1, U_2, U_3\) が、すべて \(x\) より大きくなる状況と同じになります。
つまり、
$$\begin{eqnarray}G_1(x) &=& {\rm Pr} ((U_1 > x) \cap (U_2 > x) \cap (U_3 > x))\\&=&{\rm Pr} (U_1 > x) \times {\rm Pr}(U_2 > x)\times {\rm Pr}(U_3 > x)\end{eqnarray}$$
となります。ここで、\({\rm Pr}(U_j > x) = 1 - {\rm Pr}(U_j \leq x) ~ (j = 1, 2, 3)\) となり、\({\rm Pr}(U_j \leq x)\) は、確率変数 \(U_j\) の累積分布関数に相当し、その値は区間(0, 1)において \(x\) になります(つまり、確率密度関数が "1" になる)。
したがって、累積分布関数 \(G_1(x)\) は \((1 - x)^3\) となり、確率密度関数 \(g_1(x)\) は \(3(1 - x)^2\) になります。
それでは、確率変数 \(U_1, U_2, U_3\) の中で、2番目に小さい(大きい)ものの確率密度関数はどうなるでしょうか。
最後に、その確率変数を \(X_2\) として、確率密度関数 \(g_2(x)\) を求めることを考えます。
確率密度関数は、累積分布関数の微分値に相当するので、局所的に、以下の関係が成り立ちます。
$$g_2(x) dx \approx {\rm Pr} (x < X_2 \leq x + dx)$$
つまり、累積分布関数の傾き \(g_2(x)\) に無限小区間 \(dx\) をかけ合わせたものが、\((x < X_2 \leq x + dx)\) の確率に近似できるということです。
いま、3つの確率変数 \(U_1, U_2, U_3\) を考えていて、その大小関係に基づくい並びの組み合わせを考えると、"1番小さいもの" として考えられる確率変数が3通り、"2番目に小さいもの" として考えられる確率変数が2通り、"1番大きいもの" として考えられる確率変数が1通りとなる。
仮に、"1番小さいもの" を \(Y_1\)、"2番目に小さいもの" を \(Y_2\)、"1番大きいもの" を \(Y_3\) とすると、以下のように表現することができます。
$$\begin{eqnarray}g_2(x) dx &\approx& {\rm Pr} (Y_1 \leq x) \times {\rm Pr} (x < Y_2 \leq x + dx) \times {\rm Pr} (Y_3 > x + dx)\\ &=& {\rm Pr} (Y_1 \leq x) \times {\rm Pr} (x < Y_2 \leq x + dx) \times (1 - {\rm Pr} (Y_3 \leq x + dx))\\&=&3x \times 2dx \times 1(1-x)\\&=&6x(1-x)dx\end{eqnarray}$$
したがって、確率密度関数 \(g_2(x)\) は \(6x(1-x)\) になります。

