目次(まとめ)
◾️ ランダムフォレストを構築する(要約)
◾️ 特徴の重要さは"importance"という変数に保存されている
◾️ 重要度を可視化するための関数が準備されている
◾️ 参考文献
こんにちは、みっちゃんです。
以前の記事で、決定木を組み合わせてデータを分類する手法であるランダムフォレストについて紹介しました。
今回の記事では「構築したランダムフォレストからわかることを知りたい」という方向けに、決定木の構築において、入力データのそれぞれの特徴がどれぐらい重要だったのか解説します。
ランダムフォレストを構築する(要約)
以前の記事と同様に、Rにあらかじめ準備されているアヤメのデータ(iris)を使用してランダムフォレストを構築します。
> data <- iris
> ind <- sample(nrow(data), nrow(data)*0.8)
> train_data <- data[ind,]
> test_data <- data[-ind,]
# > install.packages(randomForest) #必要の場合のみ
> library(randomForest)
> forest <- randomForest(Species~., train_data)"forest" の中身は、以下のようになっています。
> forest
Call:
randomForest(formula = Species ~ ., data = train_data)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 5.83%
Confusion matrix:
setosa versicolor virginica class.error
setosa 39 0 0 0.00000000
versicolor 0 38 3 0.07317073
virginica 0 4 36 0.10000000ここで、"OOB" とは、"Out-Of-Bag" の略であり、分類の誤り率を示しています。
ランダムフォレストでは、それぞれの決定木を構築する際に「ブートストラップ」という手法を用いて、入力データの一部を学習データに選んでいます。
したがって、それぞれの決定木によって、決定木構築に用いられた学習データは異なってきます。
そこで、ある決定木の構築に用いられた学習データ*が用いられなかった決定木(例えば、499個)からなる部分森を用いて、その学習データ*をテストデータとして部分森による分類の性能評価ができます。
その性能評価により得られた誤り率から算出されるのが、"OOB" という指標です。
特徴の重要さは"importance"という変数に保存されている
"forest" の中身を上で表示しましたが、それが全てではありません。
以下のように実行すると、"forest" にはさまざまな要素が含まれていることがわかります。
> objects(forest)
[1] "call" "classes" "confusion" "err.rate"
[5] "forest" "importance" "importanceSD" "inbag"
[9] "localImportance" "mtry" "ntree" "oob.times"
[13] "predicted" "proximity" "terms" "test"
[17] "type" "votes" "y" ※それぞれの要素の詳細については、こちらのWebサイトで説明されています(英語)。
例えば、"importance" という要素を確認したい場合には、以下のように実行します。
> forest$importance
MeanDecreaseGini
Sepal.Length 7.794777
Sepal.Width 2.597186
Petal.Length 34.449271
Petal.Width 34.434746ランダムフォレストでは、それぞれの決定木の各分岐点(ノード)において、ランダムに入力データの特徴を選択し分岐に用いています。
また、決定木では「ジニ係数」が小さくなるように分岐されます(こちらの記事をご参照ください)。
そこで、複数の決定木からなる森全体でみたときに、それぞれの特徴がどれだけジニ係数の減少に貢献したか、という情報を "importance" で示しています。
この結果から、数値が大きい「花弁の長さ(Petal.Length)」と「花弁の幅(Petal.Width)」が、ジニ係数の減少への貢献度が高いことがわかります。
また、この "importance" に関する情報は、別の関数を用いて取得することも可能です。
> importance(forest)
MeanDecreaseGini
Sepal.Length 7.794777
Sepal.Width 2.597186
Petal.Length 34.449271
Petal.Width 34.434746重要度を可視化するための関数が準備されている
上で紹介した "importance" という変数については、以下のように可視化することが可能です。
> varImpPlot(forest)出力結果は、以下のようになります。
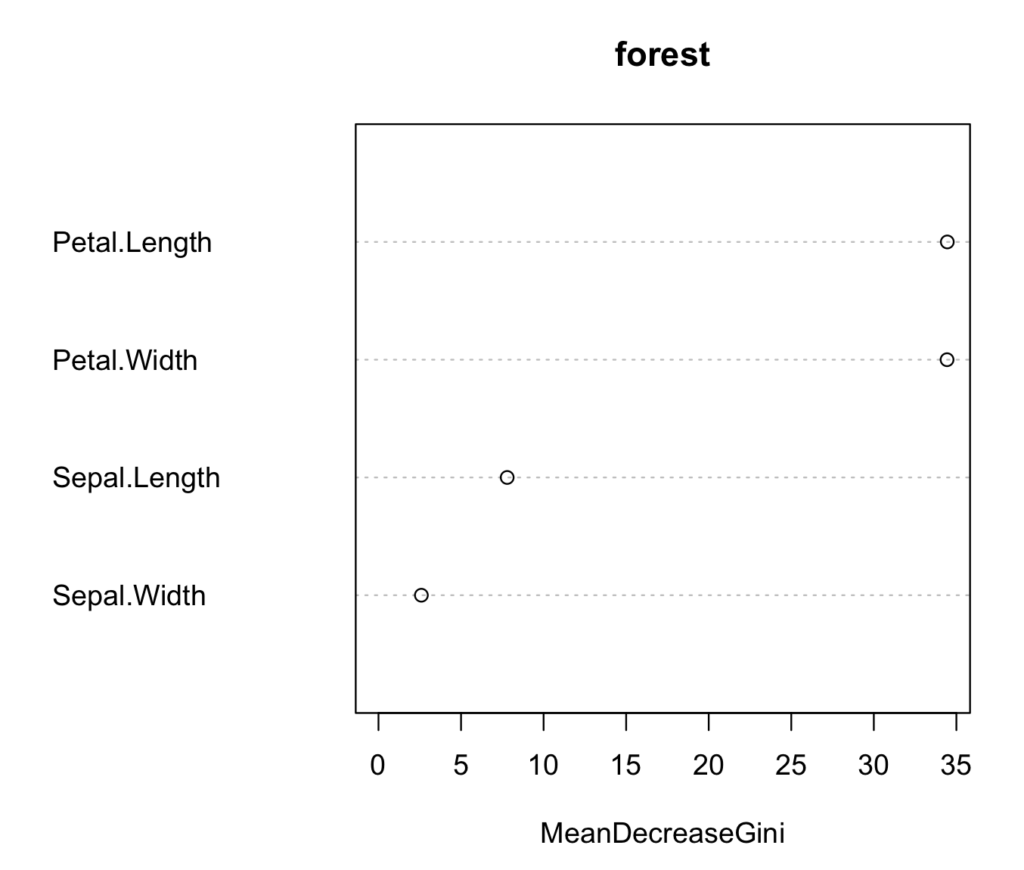
横軸に、ジニ係数の減少に貢献した重要度を示しているので、右のほうに点がある特徴が、データの分類に重要であるということがわかります。
今回の例では、入力データの特徴数が4個と少ないので、わざわざ図示しなくてもいいと思われるかもしれませんが、特徴数が多くなると、このような可視化が効果的です。

