目次(まとめ)
◾️ パレート分布の確率密度関数と平均、分散
◾️ パレート分布のパラメータが確率分布に及ぼす効果
◾️ 対数を用いた変数変換により指数分布が得られる
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、所得の分布をモデリングするために提唱された「パレート分布」について解説します。
以前紹介した「パレートの法則」と同様に、イタリア人のパレートさんによって提唱されました。
パレート分布の確率密度関数と平均、分散
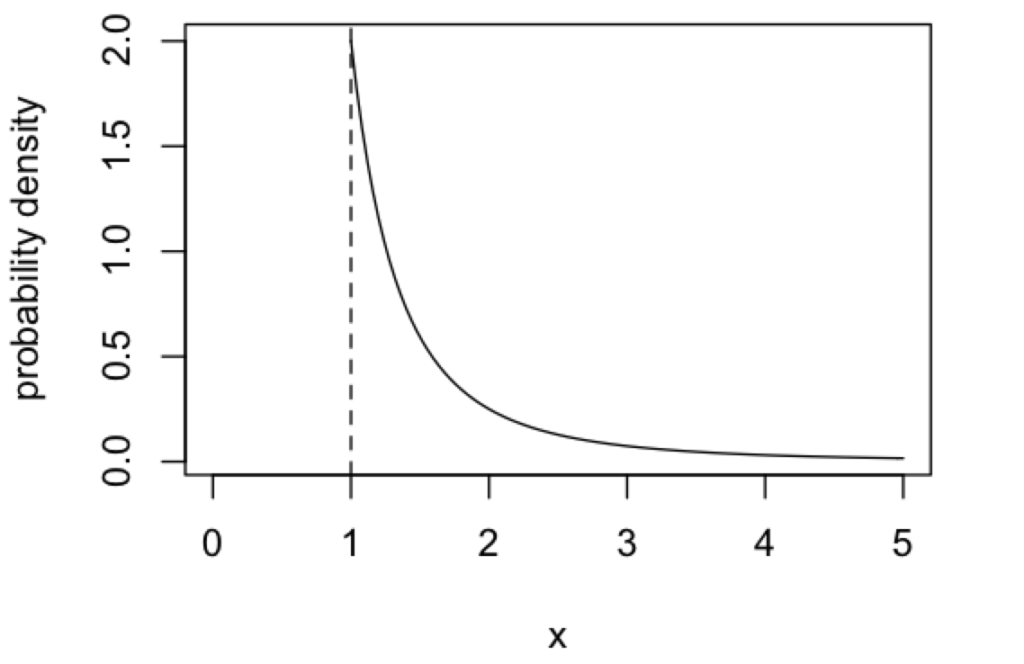
パレート分布は、尺度 \(\alpha\) (正の実数)と形状 \(\beta\)(正の実数)という2つのパラメータをつかって表現され、\(x > \alpha\) の領域で定義されます。
ちなみに、上の図で示しているパレート分布の確率密度関数は、以下のようにRで実行することで得られます(\(\alpha = 1, \beta = 2\))。
> dpareto <- function(x, alpha, beta){
> f <- (beta*alpha^beta)/(x^(beta+1))
> return(f)
> }
> curve(dpareto(x, 1, 2), xlab = "x", ylab = "probability density", xlim = c(0, 5), from = 1, to = 5)
パレート分布の確率密度関数、平均、分散は、以下のように得られます。
確率密度関数
$$f_X(x | \alpha, \beta) = \frac{\beta \alpha^\beta}{x^{\beta + 1}}$$
平均
$$E[X] = \frac{\alpha \beta}{\beta - 1}$$
分散
$${\rm Var}(X) = \frac{\alpha^2 \beta}{(\beta - 1)^2 (\beta -2)}$$
パレート分布のパラメータが確率分布に及ぼす効果
パレート分布には、尺度 \(\alpha\) と形状 \(\beta\) という2つのパラメータがあります。
まず、\(\beta = 2\) に固定して \(\alpha\) を変化させてみます。
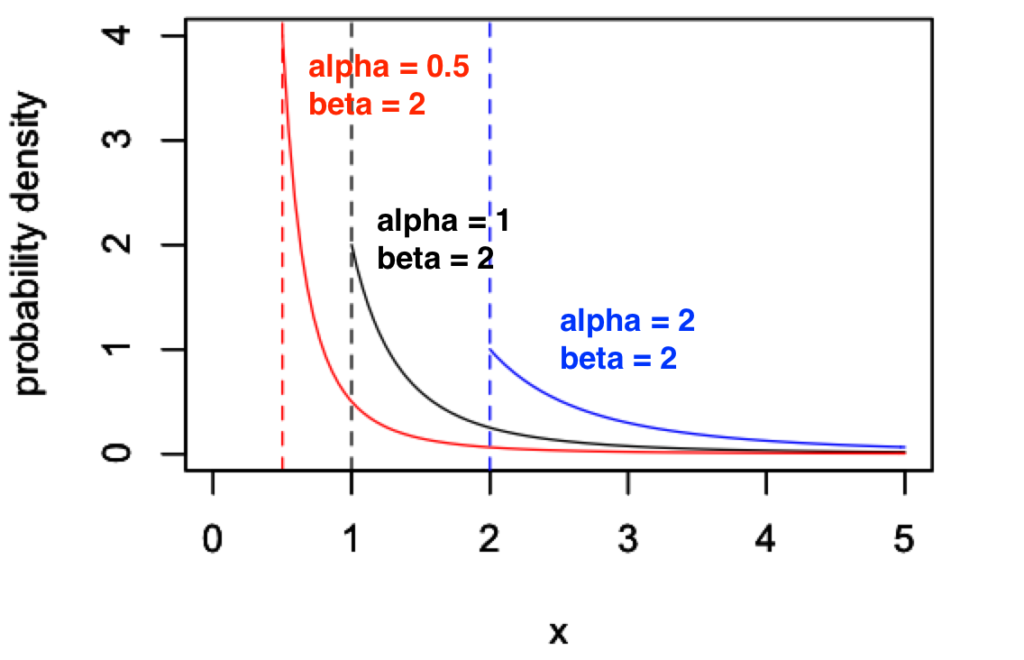
パレート分布の定義より、\(\alpha\) の値を変えると、分布の開始点が変わります。さらに、\(\alpha\) の値を大きくしていくと、なだらかな分布になることがわかります。
次に、\(\alpha = 1\) に固定して、\(\beta\) を変化させてみます。
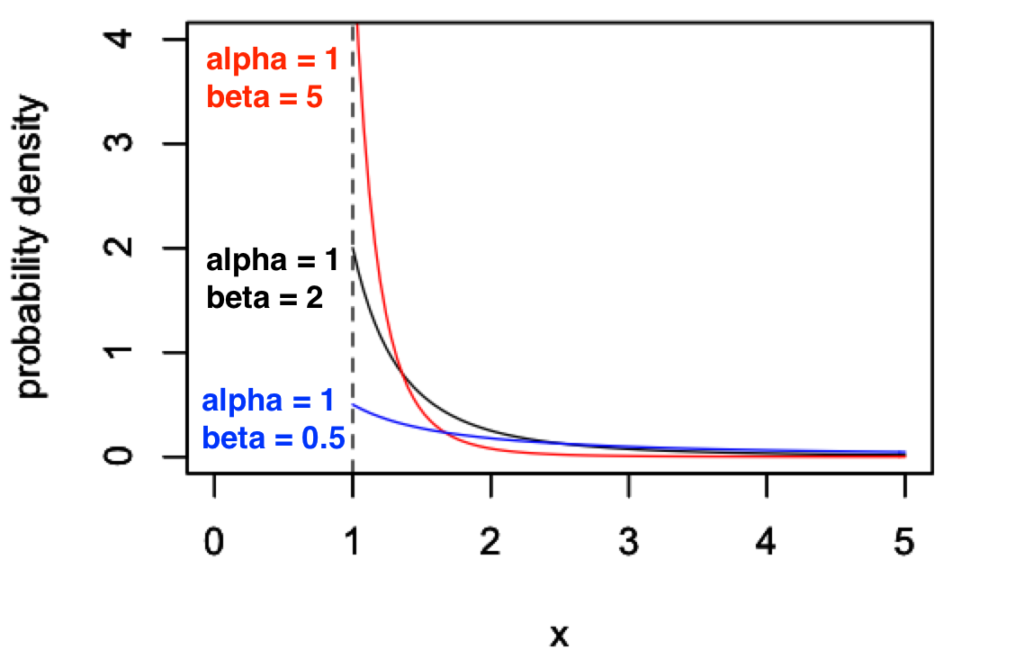
この図から、\(\beta\) を大きくしていくと、分布の開始点が上に移動していくことがわかります。
対数を用いた変数変換により指数分布が得られる
ここでは、\(Y = {\rm log}X = g(X)\) という変数変換を考えます。
この関係から、\(X = {\rm exp}\{Y\} = g^{-1}(Y)\) という関係が得られます。
公式から、\(Y\)の確率密度関数は次のように与えられます。
$$f_Y(y) = f_X(g^{-1}(y))|\frac{{\rm d}}{{\rm d}y} g^{-1}(y)|$$
したがって、パレート分布の確率密度関数 \(f_X(x | \alpha, \beta)\) について、変数変換を行うと、以下のような確率密度関数が得られます。
$$f_Y(y | \alpha, \beta) = \frac{\beta \alpha^\beta}{\{{\rm exp}\{y\}\}^{\beta + 1}} {\rm exp}\{y\} = \frac{\beta \alpha^\beta}{{\rm exp}\{\beta y\}}$$
ここで、\(\alpha = {\rm exp} \{\mu\}\)、\(\beta = \frac{1}{\sigma}\) と置いて変換すると、以下のような確率密度関数が得られます。
$$f_Y(y | \mu, \sigma) = \frac{1}{\sigma} {\rm exp}\{-\frac{y - \mu}{\sigma}\}$$
\(\mu = 0\) のときを考えると、\(\lambda = \frac{1}{\sigma}\) というパラメータをもつ指数分布になっていることがわかります(指数分布についてはこちらの記事をご覧ください)。
参考文献
久保川達也「現代数理統計学の基礎」共立出版

