行列の積は一方の列数と他方の行数が一致している必要がある【かけ算の基本】

行列のかけ算は、前の行列の列数と後の行列の行数が同じときだけ可能

まず、行列の "行" と "列" が何を意味しているのか、確認します。

行は「縦方向」、列は「横方向」に並んでいます。

したがって、「5行3列の行列」と言われたら、以下のように、縦方向に5個、横方向に3個、数字が並んでいる行列 \(A\) になります。
$$A = \left(\begin{array}{rrr}2 & 1 & -3 \\6 & 2 & -4 \\-5 & 3 & 3 \\2 & 1 & -3 \\1 & -5 & 2\end{array}\right)$$
また、「3行4列の行列」である、以下のような行列 \(B\) を考えます。
$$B = \left(\begin{array}{rrr}2 & 1 & -3 & 8\\6 & 2 & -4 & 3\\-5 & 3 & 3 & -3\end{array}\right)$$
いま、行列 \(A\) と行列 \(B\) のかけ算を考えるとき、\(A\) と \(B\) の積 \(AB\) は可能ですが、\(B\) と \(A\) の積 \(BA\) は不可能です。

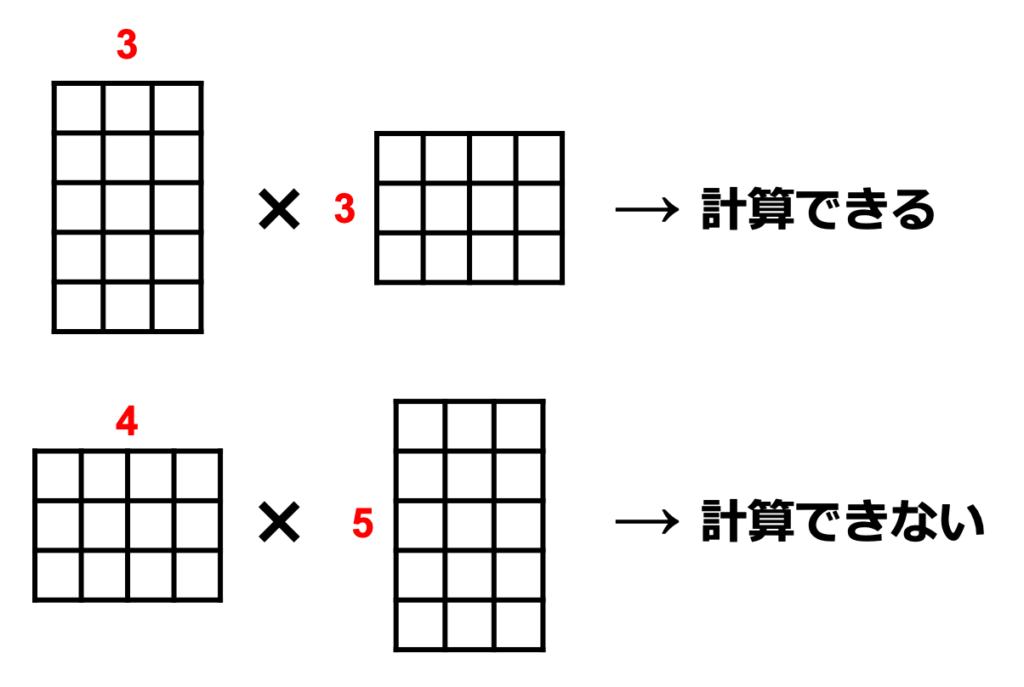
なぜなら、2つの行列のかけ算を考えるとき、前の行列の列数と、後の行列の行数が同じである必要があるためです。

\(A\) と \(B\) の積 \(AB\) の場合、前の行列 \(A\) の列数は「3」、後の行列 \(B\) の行数は「3」となり、同じ数なので、かけ算することができます。

しかし、\(B\) と \(A\) の積 \(BA\) の場合、前の行列 \(B\) の列数は「4」、後の行列 \(A\) の行数は「5」となり、同じ数ではないので、かけ算することができません。

これを忘れてしまうと、無理やり、間違った行列のかけ算をしてしまう場合があるので、覚えておきましょう。


\(A\) と \(B\) の積 \(AB\) は「5行4列の行列」になります。

「5行3列の行列」と「3行4列の行列」をかけると、「5行4列の行列」になるわけです（同じ数字のところ隠したようなイメージです）。

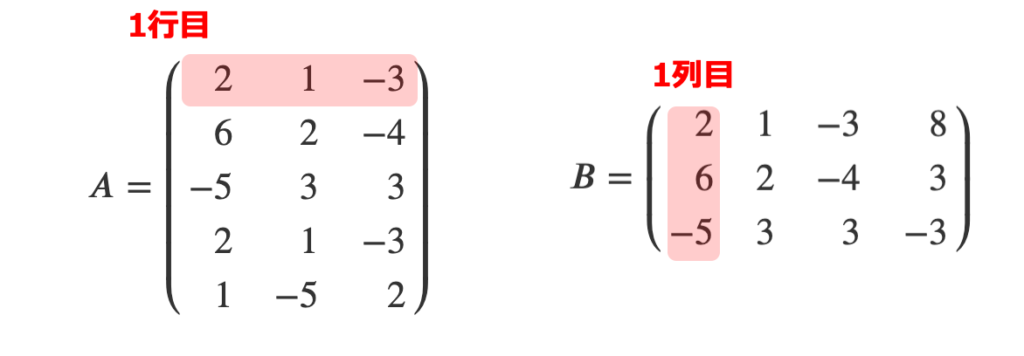
「5行4列の行列 \(AB\)」には、20個（= 5 × 4）の数字が並ぶわけですが、\(AB\) の1行1列目の数字は、\(A\) の1行目と \(B\) の1列目の数字を要素ごとにかけて足すことで出すことができます。

数字で示すと、以下のようになります。

（\(AB\)の1行目1列目の要素）= \( 2 \times 2 + 1 \times 6 + (-3) \times (-5) = 25 \)

（おまけ）LaTeXで行列を書く方法

LaTeXでは、数式をきれいに表示させることができますが、ここでは行列の書き方を紹介します。

\[
  A = \left(
    \begin{array}{rrr} % l:左構え　c:中央構え　r:右構え
      2 & 1 & -3 \\
      1 & -5 & 2
    \end{array}
  \right)
\]

表示させると、以下のようになります。
$$A = \left(\begin{array}{rrr}2 & 1 & -3 \\1 & -5 & 2\end{array}\right)$$
また、省略記号（\(\cdots, \ldots, \vdots, \ddots\)） を挿入したい場合には、以下のようなコマンドが使えます。

省略記号	意味	表示
\cdots	水平の点々（中央）	\(\cdots\)
\ldots	水平の点々（下付き）	\(\ldots\)
\vdots	垂直の点々	\(\vdots\)
\ddots	斜め右の点々	\(\ddots\)

参考文献

三宅敏恒「入門線形代数」培風館