こんにちは、みっちゃんです。
私たちが使っているコンピュータは、電源のオン「1」とオフ「0」だけの情報を用いて、複雑な処理を行っています。
このような処理のために不可欠な理論が「論理演算」です。
今回の記事では「論理演算」を行う基本的な回路「論理回路」を紹介します。
目次(まとめ)
- 論理回路は、4つの記号の組み合わせで理解できる
- フリップフロップ回路は「記憶」を担う有名な論理回路
- 参考文献
論理回路は、4つの記号の組み合わせで理解できる
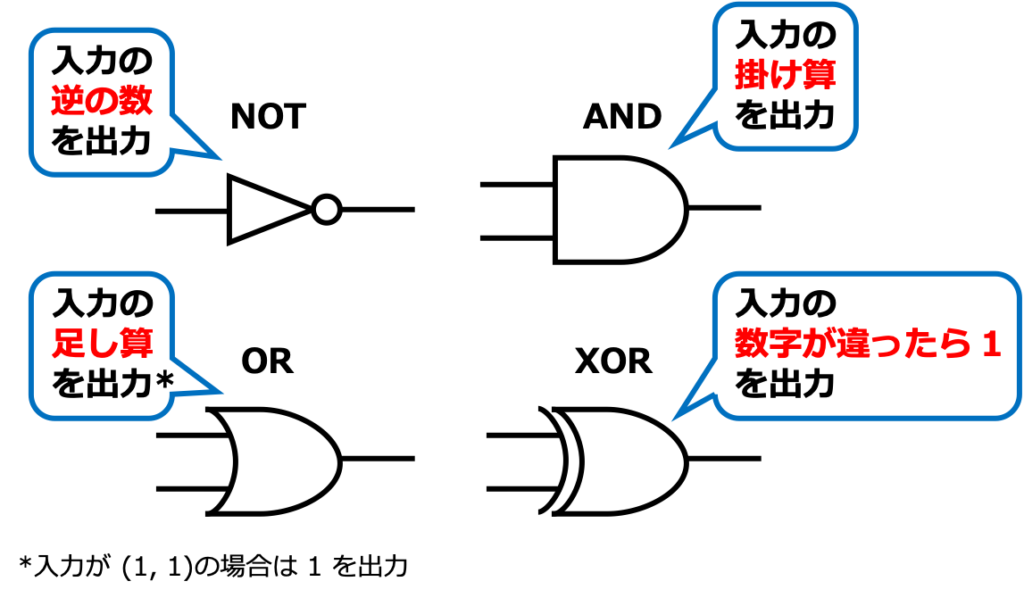
論理回路は、図に示しているような「パーツ」を使って表現します。
NOT(入力:1つ 出力:1つ)
「0」が入力されたら「1」を出力、「1」が入力されたら「0」を出力します。
AND(入力:2つ 出力:1つ)
2つの入力をいつも通り掛け算すればOKです。
1つでも「0」が入力されたら、必ず「0」が出力されます。
「0」が入力されず、「1」と「1」が入力されたら「1」を出力します。
OR(入力:2つ 出力:1つ)
2つの入力をいつも通り足し算すればOKです。
ただし、「1」と「1」が入力されたら「1」を出力することに注意が必要です。
XOR(入力:2つ 出力:1つ)
異なる数字が入力されたら「1」を出力します。
以上の4種類の記号とその意味を覚えれば、論理回路は理解できます。
また追加として、以下のように、小さい丸がついた記号が登場しますが、これは「NOT」のように、通常の逆の出力をすればOKです。
つまり、「OR」に小さい丸がついた「NOR」は、「OR」の出力を逆にする、「AND」に小さい丸がついた「NAND」は、「AND」の出力を逆にするということです。
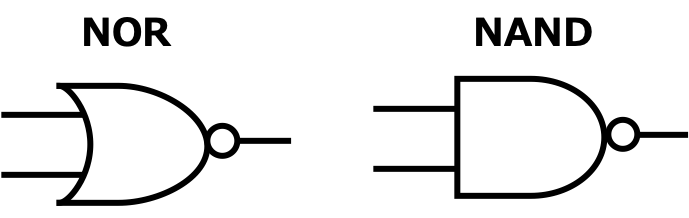
フリップフロップ回路は「記憶」を担う有名な論理回路
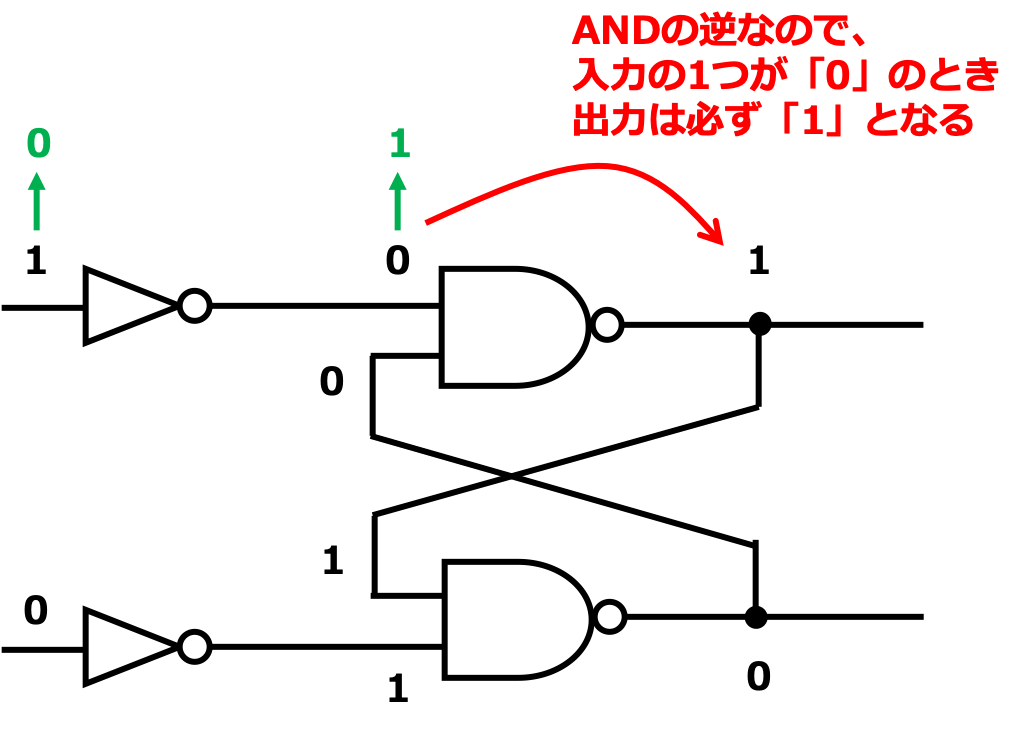
フリップフロップ回路は、上に示すように「NOT」と「NAND」の組み合わせになっている回路です。
この回路への入力は、2つあり、「1」と「0」を入力した場合(黒色)には、「1」と「0」が出力されることになります。
面白いのは、その状態で、入力を「0」「0」に変更した場合(緑色)にも、出力は変わらないという点です。
つまり、この回路の目的は「記憶」にあるわけです。
実際のコンピュータでは、メモリの一種であるキャッシュメモリで使われています。
参考文献
きたみりゅうじ「キタミ式イラストIT塾 応用情報技術者」技術評論社

