最近、いろいろなデータが観測され、その重要性が注目されています。例えば、Amazonで花子さんがパソコンを購入すると、「花子さんがパソコンを購入した」というデータをAmazonが取得します。このようなデータは、Amazonにとって、ビジネスを展開する上で貴重なものです。このような風潮から、データを取り扱った科学に取り組める人、データサイエンティストが活躍しています。
本記事では、データをモデル化(関数として表現すること)して何が嬉しいの?どうやってモデル化するの?どんなモデルがあるの?っといった疑問に答えていきたいと思います。
目次(まとめ)
- 手持ちのデータをモデル化することで未来が予測できる
- データを表現できるような直線を引くモデルが基本
- モデル構築には、最小二乗法か最尤法を適用するのが一般的
- 参考文献
手持ちのデータをモデル化することで未来が予測できる
冒頭に紹介したAmazonの例はマーケティングにおけるモデルでした。一方、自然科学の分野では、少ない観測データ(観測のための費用が高いから)から将来を予想したり、自然現象を明らかにしたりするためにモデルが作られます。
もし作ったモデルが自然現象をうまく表現できないならば、何かモデルでとらえられていない現象があると考えることができ、新たな知見を得ることができます。モデルは、試行錯誤を繰り返して精密化されるのが一般的だと思います。
データを表現できるような直線を引くモデルが基本
モデルの基本は、直線でデータを表現することです。中学校1年生でも習う単元の1つですが、"比例"と言われる関係も直線関係と言えます。
学年を経るごとに、二次関数や三次関数など、直線が曲線に変わっていくと思います。これは、実際に身の回りで起きる現象を直線関係だけで表現することは難しいからです。
ただし、曲線的なモデル(非線形モデル)を考えるときにも、直線的なモデル(線形モデル)の理解が基本になります。
モデル構築には、最小二乗法か最尤法を適用するのが一般的
モデルを構築する作業は、"回帰係数"を探索する作業と同じです。回帰とは、モデルをデータに当てはめるという意味で、回帰係数とは、データに当てはまるようなモデル中の係数(パラメータ)のことを意味します。
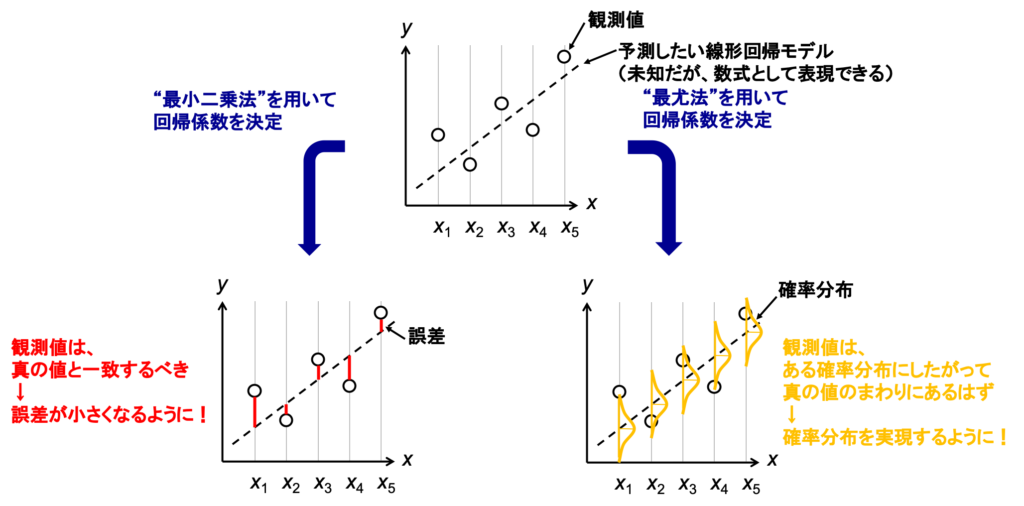
回帰係数を探索、決定するための手法として、主に、「最小二乗法」と「最尤法」があります(図1を参照してください)。ここでは、直線的なモデルについて考えるので、図に示しているように点線を表現するような数式を決定、つまり、数式中の回帰係数を決定することが目標です。
最小二乗法では、「観測値は、回帰直線上の値と一致するべきだな」と考えます。観測値には、観測する際のノイズが含まれるので、図中の赤色で示しているような誤差が生まれます。逆に言えば、観測値からみて誤差が小さくなるような回帰直線を描ければよいので、それを表現するような数式が設計され、回帰係数が決定されます。
最尤法では、「観測値は、回帰直線上の値から、確率的に散らばっているんだな」と考えます。私は確率の単元を苦手にしてきたので、"確率的"と聞くだけでちょっと身構えしてしまう方の気持ちもわかります。ただ、やっていることは単純です。観測値は、高い確率で回帰直線上にあるはずなんですが、低い確率で回帰直線から外れてしまうこともあるということです。
確率が高いか低いかを表現するのが、図のオレンジ色で示しているような確率分布です。山が並んでいますが、山の頂上のところが「確率が高い」ことを示しています。確率分布には、いろいろな種類があり、それぞれに対して式が分かっています(統計検定などでは覚えておく必要があります)が、一般的には、正規分布が用いられます。
正規分布の式を、回帰係数を含むように式変形することで、確率が高くなるように回帰係数を決定します。
詳しい数式は、参考文献などをご参照ください。
参考文献
小西貞則「多変量解析入門 ー線形から非線形へー」岩波書店

