目次(まとめ)
◾️ 度数分布表を作成し、数値データを分類する
◾️ ヒストグラムを用いて、度数分布表を可視化する
こんにちは、みっちゃんです。
わたしたちは、普段生活する中で、多くの数字に遭遇します。
例えば、コンビニエンスストアに入ると、"110円" のおにぎり、"200円" のお茶、"50円" のお菓子、などさまざまな値段のついたものが並んでいます。
また、投票にいくと、その結果として、A候補の得票数は "1000票"、B候補の得票数は "1400票"、C候補の得票数は "3000票" といったように、さまざまな得票数が得られます。
このように、さまざまな数値データを扱うのが「統計」ですが、数値データをまとめて表示した表が「度数分布表」、さらにグラフとして可視化したのが「ヒストグラム」です。
今回の記事では「度数分布表」と「ヒストグラム」の関係について、解説していきます。
度数分布表を作成し、数値データを分類する
ここでは、説明のため、以下のような数値データがあるとします。
6.2658858, 8.0526865, 3.9419547, 7.4756913, 8.7231253, 7.0644387, 2.7964198, 0.9280137, 3.1400580, 1.2473234ちなみに、この数値データは、以下のように、Rの一様乱数(0〜10の範囲で10個)を使って作っています(Rについては、こちらの記事をご参照ください)。
> num <- runif(10, 0, 10)このデータから、度数分布表は、以下のように書くことができます。
| 階級 | 度数 |
|---|---|
| 0 〜 1 | 1 |
| 1 〜 2 | 1 |
| 2 〜 3 | 1 |
| 3 〜 4 | 2 |
| 4 〜 5 | 0 |
| 5 〜 6 | 0 |
| 6 〜 7 | 1 |
| 7 〜 8 | 2 |
| 8 〜 9 | 2 |
| 9 〜 10 | 0 |
やっていることは簡単で、まず「階級」を設定して、それぞれの階級の中に入る数値を「度数」として数え上げるだけです。
ここでは「階級」を10個設定していることになります。
この表を見ると、"3〜4"、"7〜8"、"8〜9" の範囲に、比較的多く(2個)の数値が含まれていることがわかります。
ヒストグラムを用いて、度数分布表を可視化する
ヒストグラムは、Rをつかって、以下のように描くことができます。
> hist(num, breaks=seq(0, 10, 1))ここで、"num" には上で設定した10個の数字、"breaks" で階級を指定しています。
"seq(0, 10, 1)" とすることで、"0" から "10" の範囲で "1" の幅で、階級を設定することができます。
これを実行すると、以下のように「ヒストグラム」を描くことができます。
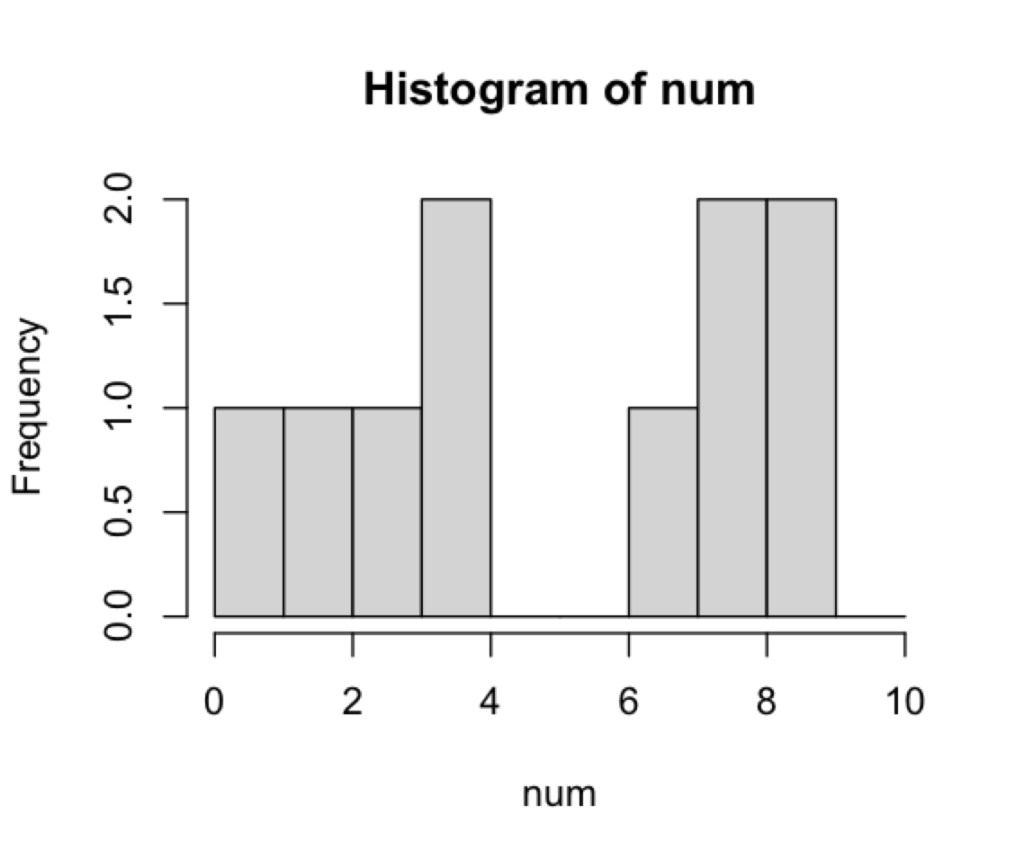
この図からも、"3〜4"、"7〜8"、"8〜9" の範囲に、比較的多く(2個)の数値が含まれていることがわかります。
例えば、階級の幅を "0.5" にしたければ、以下のように実行します。
> hist(num, breaks=seq(0, 10, 0.5))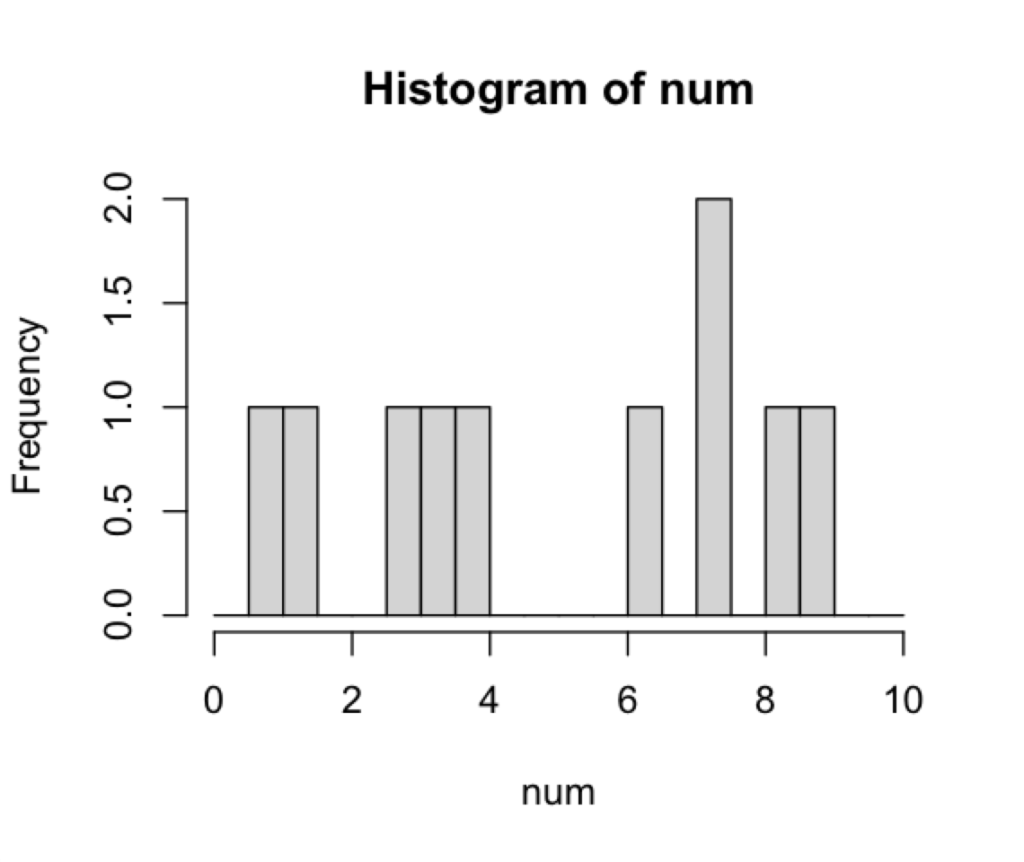
このように図示すると、"0.5" の幅で階級を分けたときに、"7.0〜7.5" の範囲の数値が2個あることが、簡単にわかります。
度数分布表を書くのは大変かもしれませんが、ヒストグラムを描けば、数値の分布を簡単に把握することができます。
また、ヒストグラムの詳細のデータは、以下のように得ることができます。
> (hist(num, breaks=seq(0, 10, 0.5)))
$breaks
[1] 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
[16] 7.5 8.0 8.5 9.0 9.5 10.0
$counts
[1] 0 1 1 0 0 1 1 1 0 0 0 0 1 0 2 0 1 1 0 0
$density
[1] 0.0 0.2 0.2 0.0 0.0 0.2 0.2 0.2 0.0 0.0 0.0 0.0 0.2 0.0 0.4 0.0 0.2 0.2 0.0
[20] 0.0
$mids
[1] 0.25 0.75 1.25 1.75 2.25 2.75 3.25 3.75 4.25 4.75 5.25 5.75 6.25 6.75 7.25
[16] 7.75 8.25 8.75 9.25 9.75
$xname
[1] "num"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
