こんにちは、みっちゃんです。
今日は、「次元」という概念、また、「次元」を落としてデータを判別する技術である「正準判別」について紹介したいと思います。
目次(まとめ)
- わたしたちの生活は高次元データで特徴づけられている
- 高次元データを低次元データで表現するための次元圧縮
- 正準判別分析は次元圧縮を用いた判別を行う
- 参考文献
わたしたちの生活は高次元データで特徴づけられている
例えば、AくんとBくんを、その特徴から区別したいという状況を考えます。
まず、それぞれの性別だけに注目しようとすると、Aくん=男、Bくん=男、となり、AくんとBくんを区別することができません。
これは、「性別」という1つの次元に対応する軸だけを用いて、AくんとBくんを区別しようとして、区別できなかったことを意味します。
次に、それぞれの「性別」に加え、「趣味」にも注目したらどうでしょうか。
仮に、Aくん=(男、映画)、Bくん=(男、映画)となったとき、やはり、AくんとBくんを区別することができません。
これは、「性別」「趣味」という2つの次元に対応する軸を用いてAくんとBくんを区別しようとして、やはり区別できなかったことを意味します。
さらに、それぞれの性別、趣味に加え、身長にも注目するとどうでしょうか。
仮に、Aくん=(男、映画、160cm)、Bくん=(男、映画、180cm)となったとき、AくんとBくんを区別することができます(身長差から区別できる)。
これは、「性別」「趣味」「身長」という3つの次元に対応する軸を用いて、AくんとBくんを区別しようとして、無事に区別できたということを意味します。
この例から分かるように、わたしたちの身の回りの多くは、高い次元で表現されなければ判別(区別)できません。
高次元データを低次元データで表現するための次元圧縮
わたしたちは、高次元データを理解することを苦手にしています。
なぜなら、データが高次元になればなるほど、その視覚化が難しいからです。(一般的に馴染みがあるのは3次元以下のデータだと思います)
そこで、高次元データを低次元データで表現して、わたしたちが理解しやすくする手法として、「次元圧縮」という手法があります。
例えば、\((x_1, x_2, x_3)\)という3次元で表現されたデータ(例えば、Aさんの国数英の点数)を、\((y_1, y_2)\)という2次元で表現するため、以下のような式が与えられたとします(※係数は適当です)。
$$y_1 = 2.5x_1 + 1.2x_2 + 5.3x_3\\y_2 = 2.2x_1 + 0.2x_2 + 2.7x_3$$
この式が与えられれば、2つの式に\((x_1, x_2, x_3)\)の値を代入すれば、\((y_1, y_2)\)が算出できます。
これは、3次元のデータを2次元に変換できた、つまり、次元圧縮できたことを意味します。したがって、逆に言うと、次元圧縮したいと思えば、式中の係数を決めればいいということになります。
正準判別分析は次元圧縮を用いた判別を行う
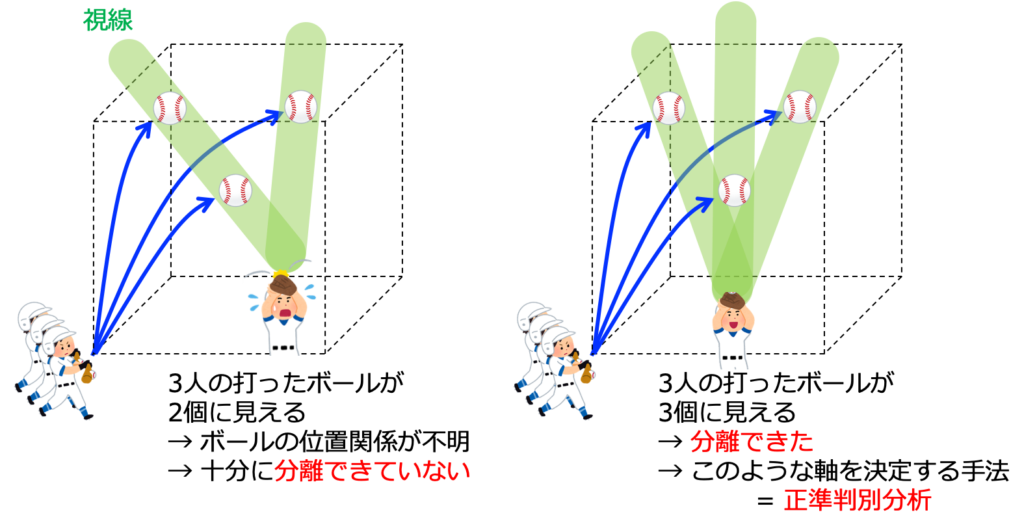
正準判別では、次元圧縮を用いて、高次元空間に存在する様々な群のデータの位置関係を捉えて、分離します(線形判別分析との違いは、判別する群の数)。
参考文献において、著者は、野球のボールの例を挙げているので、ここでは、その状況を図示しています(図1参照)。図1は、複数のバッターが打った3つのボールが空中にあるとき、場所(守備位置)によっては、ボールが重なり、3つのボールの位置関係が判別できない状況になることを示しています。
正準判別では、3つのボール、つまり、3つの群を判別できるような軸を決定することが目的となります。
詳細な数式に興味のある方は、参考文献をご覧ください。
参考文献
小西貞則「多変量解析入門 ー線形から非線形へー」岩波書店

