目次(まとめ)
◾️ ベータ分布の確率密度関数と平均、分散
◾️ ベータ分布のパラメータが確率分布に及ぼす効果
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、0から1の値を示す確率変数の分布である「ベータ分布」について解説します。
ベータ分布の確率密度関数と平均、分散

ガンマ分布は、形状母数\(\alpha\)と尺度母数\(\beta\)という2つのパラメータ、および、ガンマ関数 \(\Gamma (\alpha)\) をつかって表現されていました(詳細はこちらの記事をご覧ください)。
同様に、ベータ分布は、\(a\) と \(b\) という2つのパラメータ、および、ベータ関数 \(B(a, b)\) をつかって表現されます。
ちなみに、上の図で示しているベータ分布の確率密度関数は、以下のようにRで実行することで得られます(\(a = 3, b = 2\))。
> curve(dbeta(x, 3, 2), xlab = "x", ylab = "probability density", xlim = c(0, 1))ベータ分布の確率密度関数は、以下のように得られます。
確率密度関数
$$f_X(x | a, b) = \frac{1}{B(a, b)} x^{a-1} (1-x)^{b-1}$$
ここで、\(B(a, b)\)はベータ関数と呼ばれる関数で、以下のように定義されます。
$$B(a, b) = \int_{0}^{1} x^{a-1} (1-x)^{b-1}dx$$
ベータ関数は、以前の記事で紹介したガンマ関数を使って以下のように表現することもできます。
$$B(a, b) = \frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}$$
また、ベータ分布の平均は \(\frac{a}{a+b}\)、分散は \(\frac{ab}{(a+b)^2(a+b+1)}\) になります。
ベータ分布のパラメータが確率分布に及ぼす効果
ベータ分布には、\(a\) と \(b\) という2つのパラメータがあります。
まず、\(b = 1\) に固定して \(a\) を変化させてみます。
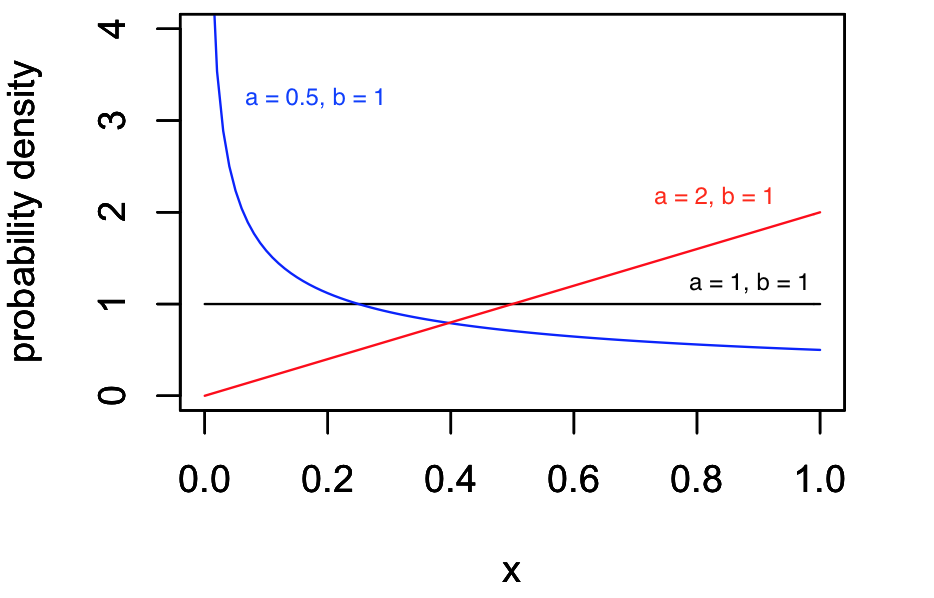
この図から、\(a\) の値が小さいときは左肩あがりの曲線になり、\(a\) を大きくしていくと、右肩上がりの曲線に変わっていくことがわかります。さらに、\(a\) を大きくしていくと、青線を反転させたような曲線になります。
次に、\(a = 1\) に固定して、\(b\) を変化させてみます。
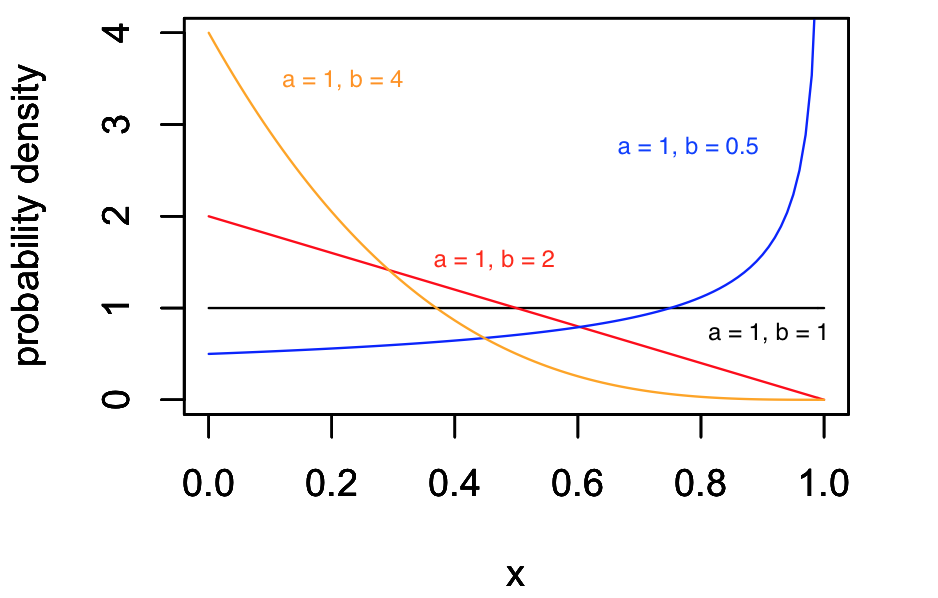
この図から、\(a\) の場合とは逆に、\(b\) の値が小さいときは右肩あがりの曲線になり、\(b\) を大きくしていくと、左肩上がりの曲線に変わっていくことがわかります。
ちなみに、\(a\) も \(b\) も1より小さい値をとるような場合には、以下のようにお椀型の曲線となります。
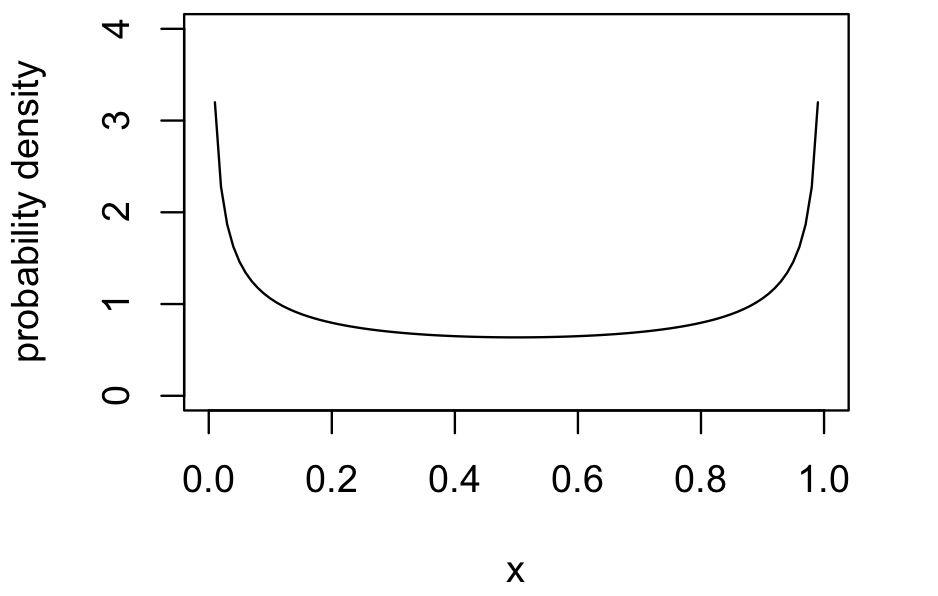
参考文献
久保川達也「現代数理統計学の基礎」共立出版

