こんにちは、みっちゃんです。
今回の記事では、情報処理試験で出題される「アローダイアグラム」の解き方について解説したいと思います。
紹介するシンプルな解き方を理解できれば、怖いもの無しです。
※説明のため、きたみりゅうじさんの著書で取り上げられているデータを使用させていただいています。内容の詳細は、参考文献をご参照ください。
目次(まとめ)
- アローダイアグラムは作業の流れを所要時間とともに示した図
- アローダイアグラムの難しさは「作業の開始と終了」をつないでいくことにある
- アローダイアグラムの問題は、所要時間を足していけば簡単に解ける
- 参考文献
アローダイアグラムは作業の流れを所要時間とともに示した図
例として、システム開発のために以下のような作業があるとします。
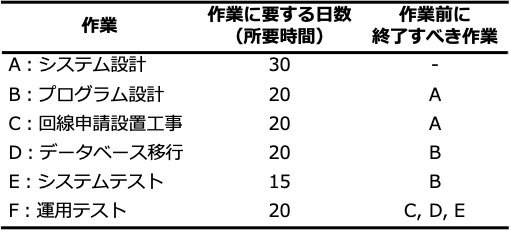
それぞれの作業について、それを行うための所要時間(ここでは日数)や、それを行う前に終了しておかなければならない作業がわかっています。
このようなデータをよりわかりやすく表示するために提案された図が、以下に示すような「アローダイアグラム」です。
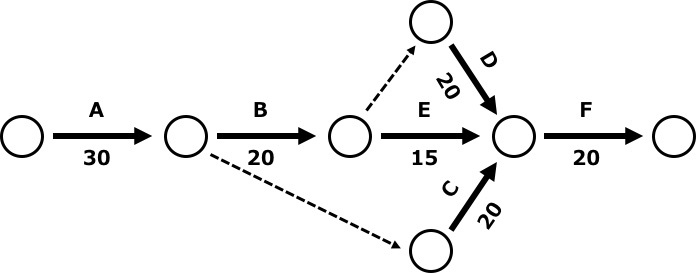
アローダイアグラムの難しさは「作業の開始と終了」をつないでいくことにある
アローダイアグラムですが、初めて見た方の感想はどうでしょうか?
私は最初に見たとき「なんじゃこれ」という感じで、読み方がよくわかりませんでした。
おそらく多くの方は、最初に示した表から以下のような図を思い浮かべるかなと思います。
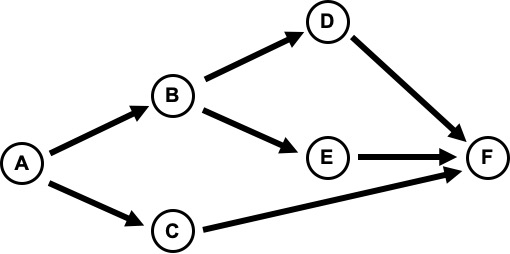
ただこの図では、「作業の流れ」は分かるけれども、「所要時間」の情報をうまく反映できないという問題があります。
アローダイアグラムは、この図の中で、「○を→に」「→を○に」入れ替えたようなイメージで描かれています。
結果として、アローダイアグラムが示す「○」は、作業の開始と終了を表す記号(結合点)という意味を持っています。
アローダイアグラムの問題は、所要時間を足していけば簡単に解ける
情報処理試験では、以下のようなアローダイアグラムについての問題が出題されています。
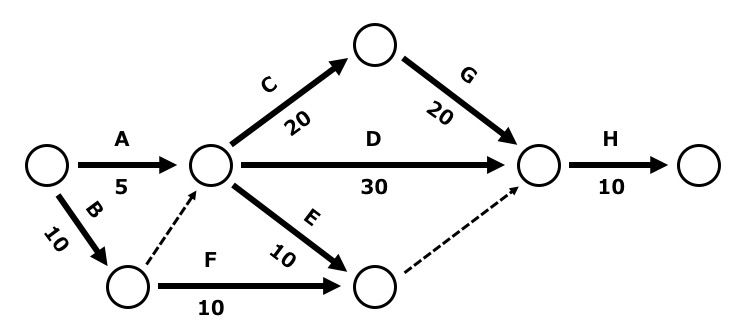
わたしがお勧めする解き方は、矢印(→)を辿りながら、すべての丸(○)に「そこに到達するための日数」を記入していくことです。
そのとき考えるのは、それぞれの丸に入ってきている矢印です。
また、点線については、所要日数ゼロとして計算します。
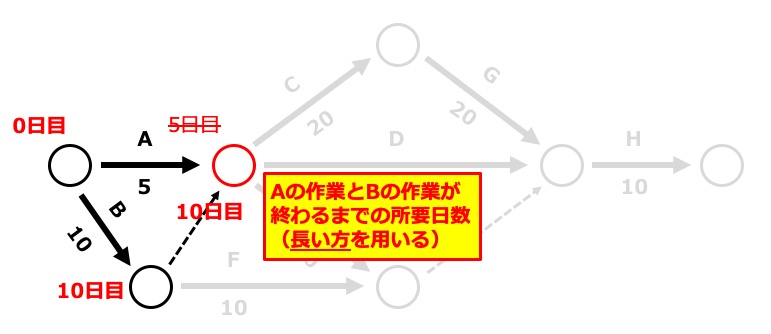
このように全ての丸について、所要日数を記入すると、以下のようになります。
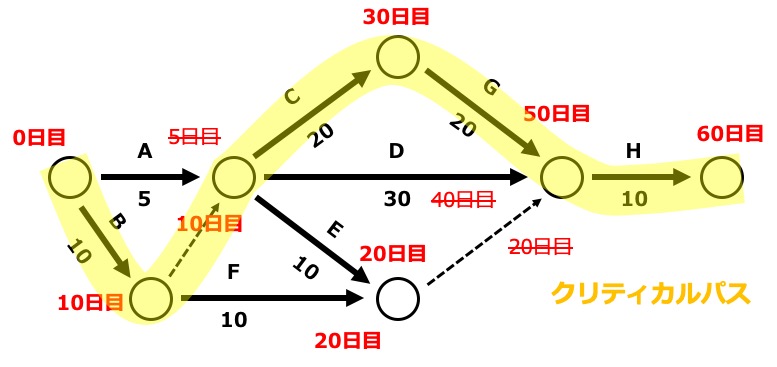
図の中で、全体の所要時間を決めている経路を「クリティカルパス」といいます。
【例題】
(1) 作業Eの余裕日数は何日か?
作業Eの開始が10日目であること、作業Hの開始である50日目に間に合わせないといけない作業であることから、作業Eに与えられた時間は40日。作業Eは、もともと10日を要する作業なので、余裕日数は30日(=40−10)。
(2)作業Fを最も遅く開始できるのは何日目か?
作業Fの開始が10日目以降であること、作業Hの開始である50日目に間に合わせないといけない作業であることから、遅くとも40日目に作業Fを始めればよい。
みなさんもアローダイアグラムマスターになってください。
参考文献
きたみりゅうじ「キタミ式イラストIT塾 応用情報技術者」技術評論社

