こんにちは、みっちゃんです。
これまでの記事で、2回にわたって「決定木」について紹介してきました。
- Yes/Noチャートを使ってデータを分類する【決定木】
- データ読み込みから決定木の可視化まで解説【Pythonをつかいます】
今回の記事では、決定木によるデータ分類のための指標である「ジニ係数」、可視化した決定木の見方、などについて解説したいと思います。
目次(まとめ)
- 決定木では、「はい」か「いいえ」を辿りながらデータを分類
- 決定木は、ジニ係数が小さくなるようにデータを分類している
- ジニ係数は、不純度や不平等度を示す指標
- 参考文献
決定木では、「はい」か「いいえ」を辿りながらデータを分類
説明のため、以前の記事で用いた入力データと可視化した決定木を、それぞれ図1、図2として示します。
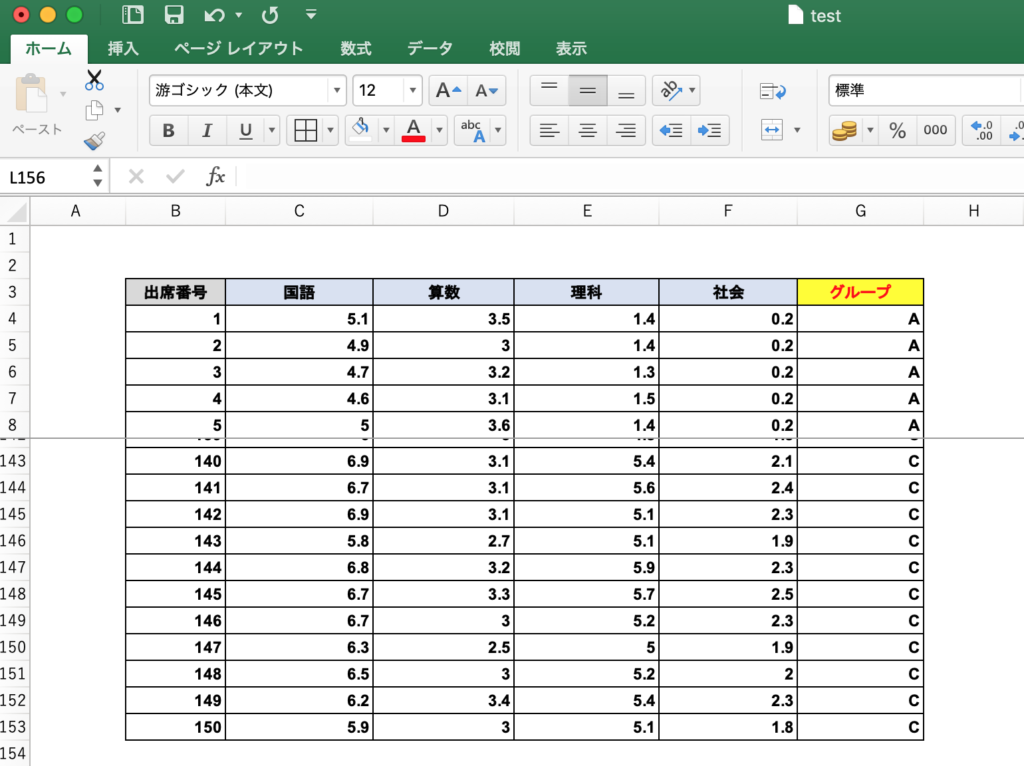
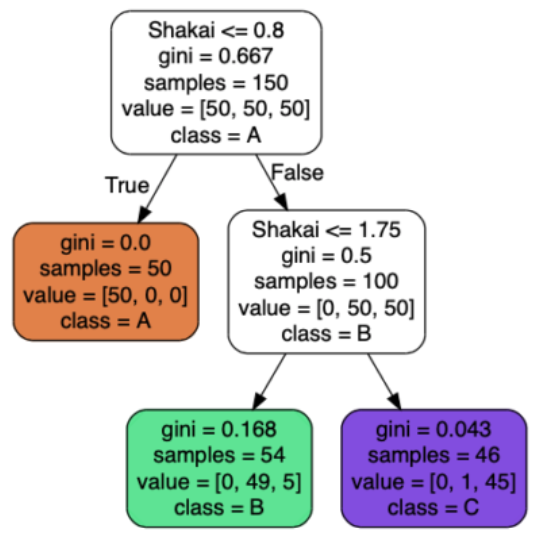
ここでは、出席番号1番の生徒さんの点数(国語:5.1点、算数:3.5点、理科:1.4点、社会:0.2点)を考えて、この生徒さんのグループを決定木で分類できるか確認します。
決定木は上から見ていきます。
「Shakai <= 0.8」とは「社会の点数が0.8以下」という意味で、あてはまる(はい)ならば"True"を、あてはならない(いいえ)ならば"False"の矢印を進みます。
「gini = 0.667」とは「ジニ係数が0.667」であることを示していて、「samples = 150」とは「この箱(ノード)に分類される生徒の数が150人」であることを示しています(分類前なので全員です)。
「value = [50, 50, 50]」とは「50人の生徒がグループA、50人の生徒がグループB、50人の生徒がグループC」であることを意味しています([A, B, C]の人数の内訳です)。
「class = A」とは、もし「社会の点数が0.8以下」という条件にあてはまる生徒がいれば「Aに分類する」という意味です。
出席番号1番の生徒さんの社会の点数は0.2点なので、「社会の点数が0.8以下」の条件にあてはまり、オレンジ色のノードに分類されます。
このように決定木を眺めると、以下のことがわかります。
- 緑色のノードには、Bグループとして54人(sample)が分類されたけれど、valueをみると、本当は54人のうち49人はBグループで、残り5人はCグループであることがわかる。つまり、5人は間違ってBグループに分類されてしまった、ということを意味している。
- 紫色のノードには、Cグループとして46人(sample)が分類されたけれど、valueをみると、本当は46人のうち45人はCグループで、残り1人はBグループであることがわかる。つまり、1人は間違ってCグループに分類されてしまった、ということを意味している。
決定木を作るという作業は、データを正しくグループ分けできるように条件(質問内容)を決めるということ対応します。
決定木は、ジニ係数が小さくなるようにデータを分類している
上の決定木にも書いてあるように、決定木は、一般的に、ジニ係数を指標に構築されます。
具体的には、ジニ係数が小さくなるようにデータを決定木を構築します。
上の例では、分類前のすべてのデータに対するジニ係数が「0.667」であり、分類後には、Aグループで「0.0」、Bグループで「0.168」、Cグループで「0.043」というふうに小さい値をとるようになっています。
ジニ係数(Gini index)の求め方は、以下の通りです。
$$({\rm Gini}) = 1 - \sum_{i=1}^c {p_i}^2$$
ここで、\(c\)は「グループの数」、\(p_i\)は「全データ数に対するあるグループのデータ数」を示しています。
ジニ係数は、不純度や不平等度を示す指標
ジニ係数は、決定木においては、ノード内のデータの不純度を評価する指標として用いられています。つまり、同じグループに属するデータのみからなるノードの不純度はゼロとなります。
ジニ係数は、収入などの不平等度を評価する際にも用いられます。
例えば、累積世帯比率を横軸に、累積所得比率を縦軸にとって描いたローレンツ曲線では、図3に示すようにジニ係数を計算することができます。
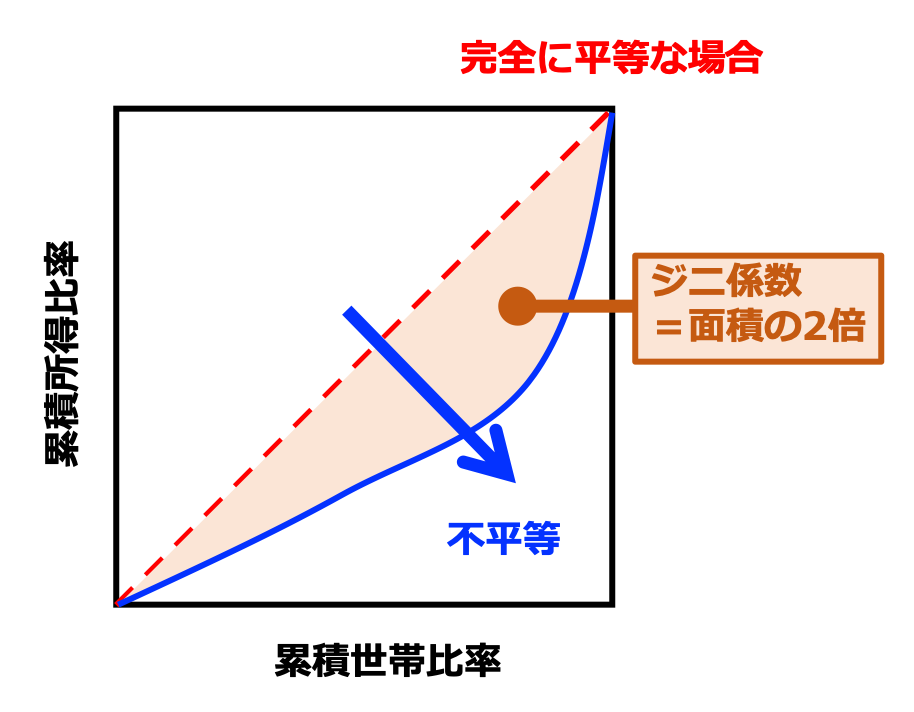
このことに関しては、統計検定でも問われることなので、是非覚えておくといいと思います。
参考文献
- 平井有三「はじめてのパターン認識」森北出版
- 久保川達也「現代数理統計学の基礎」共立出版

