こんにちは、みっちゃんです。
これまでの記事で、異なるグループに属するデータを分けるための手法として、サポートベクトルマシン(SVM; Support Vector Machine)などを紹介してきました(こちらを参照)。
その際、基本を理解するという目的のため、「異なるグループのデータを直線を引いて分けることができる」ということを想定してきました。
しかし、直線では分けることができないデータのときは、どうしたらいいのでしょうか?
本記事では、そのような状況を打開する戦略、その際に生じる課題を解決する方策としてのカーネル法について解説したいと思います。
目次(まとめ)
- データを高次元の中で考えることで、データを直線で分けられるようになる
- 高次元になればなるほど、計算が不可能になるという問題が生じる
- カーネル法は、不可能と思われた計算を可能にする仕掛け
- 参考文献
データを高次元の中で考えることで、データを直線で分けられるようになる
一般に、データの次元が、データの数より大きくなれば、データを直線でグループ分けできるようになることが知られています。
例えば、国語、算数、理科、社会、英語という5科目の点数からなるデータがあったとします。これは、5次元のデータといいます。このデータが3人分しかなければ、(データの次元:5)>(データの数:3)となるので、そのままのデータを使えば、直線でグループ分けできることが予想できます。
しかし、もし40人分あったらどうでしょうか?
この場合には、(データの次元:5)>(データの数:40)が成り立たないので、このままでは、直線でグループ分けできないと予想できます。
そこで、データの次元を"あえて"高くするという処理を行えばいい、という発想になるわけです。上の例では、次元が40より大きくなる処理を、データに施すということです。
高次元になればなるほど、計算が不可能になるという問題が生じる
しかし、データが高次元になるほど、計算が難しくなることは予想できます。
むしろ、以前の記事で次元圧縮に基づく正準判別ついて解説したように、次元を下げることが通常目指すべき方向であり、次元を上げることは、それに逆行しているようにも感じます。
実際に、上の例でも、もともと5次元だったデータを40次元以上のデータとして取り扱おうとしています。場合によっては、無限次元まで高次元にしなければ、計算が行えないような状況に陥ってしまいます。
カーネル法は、不可能と思われた計算を可能にする仕掛け
データを高次元の中で表現することによって生じる計算の問題を解決するために、「カーネル法」という手法が用いられます。特に、サポートベクトルマシンの分野では「カーネルトリック」として知られます(こちらの方が有名かもしれません)。
まず、説明のために「関数」について説明したいと思います(図1)。
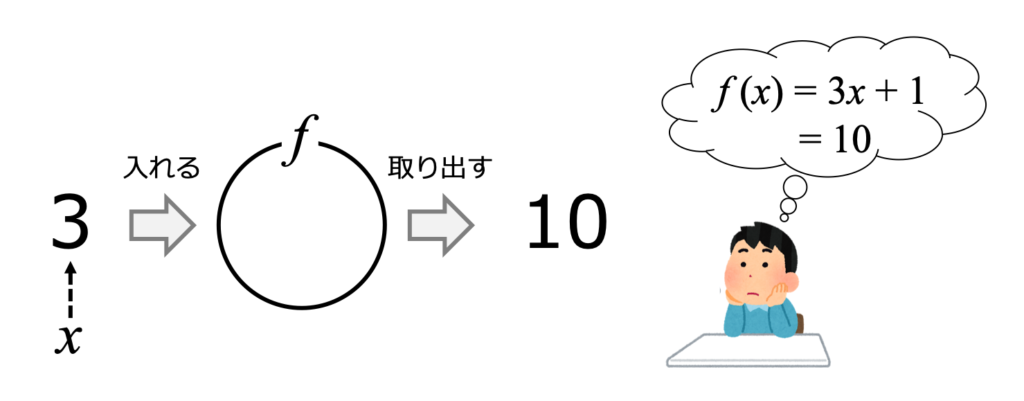
関数(function)とは、何かの処理を施す袋のようなものです。この例の場合には、いろいろな関数が考えられますが、図の中の少年は「入れた数字を3倍にして1を足してくれる」関数を想定しているようです。
同様に、以下のような状況を考えます(図2)。
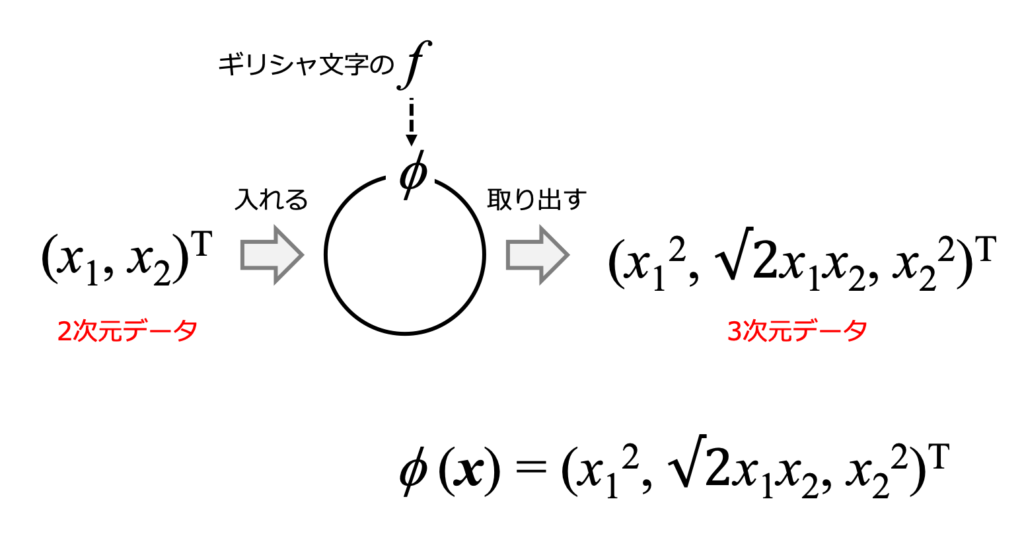
ここでは、2次元のデータを3次元のデータに変換するという操作を、関数が担っています。
以下に、\({\bf x} = (x_1, x_2)^T\)と\({\bf y} = (y_1, y_2)^T\)というデータを、関数\(\phi\)に入れた時に取り出されるデータをまとめます。
$$\phi ({\bf x}) = ({x_1}^2, \sqrt{2}x_1x_2, {x_2}^2)^{\rm T}\\
\phi ({\bf y}) = ({y_1}^2, \sqrt{2}y_1y_2, {y_2}^2)^{\rm T}$$
実用上の計算では、これらの"内積"を計算する必要があるので、計算してみます。
$$
\begin{eqnarray}
\phi ({\bf x})^{\rm T}\phi ({\bf y}) &=& {x_1}^2{y_1}^2 + \sqrt{2}x_1x_2\sqrt{2}y_1y_2 + {x_2}^2{y_2}^2\\
&=& (x_1y_1 + x_2y_2)^2\\
&=& ({\bf x}^{\rm T}{\bf y})^2
\end{eqnarray}
$$
こうすると不思議なことに、高次元にしたデータ(3次元のデータ)を使って計算した内積が、もとのデータ(2次元のデータ)を使って計算できる内積とよく似ていることがわかります。
これがカーネル法のエッセンスです。
ちなみに、\(({\bf x}^{\rm T}{\bf y})^2\)は、「多項式カーネル」として知られています。他にも、代表的なカーネル関数として、「ガウスカーネル」や「シグモイドカーネル」があります。
また、このような変換は「Mercerの定理」という定理で保証されています。
興味のある方は、参考文献などをご参照ください。
参考文献
小西貞則「多変量解析入門 ー線形から非線形へー」岩波書店

