こんにちは、みっちゃんです。
複雑なデータに出会った時、そのデータの解釈は十分にできていますか?
複雑さを軽減するために、あらかじめ必要そうなものを自ら(恣意的に)選んだりしていないでしょうか?
今回の記事では、ビッグデータ解析の定番である「主成分分析」を紹介します。
「主成分分析」をマスターすれば、複雑なデータも、目に見える形で解釈できるようになります。
目次(まとめ)
- 主成分分析を活用して、複雑なデータを解釈しやすくできる
- 主成分分析の基本は、データの散らばりを大きくするような係数を見つけること
- 主成分分析はさまざまなプログラミング言語で実行可能(Pythonを例に解説)
- 参考文献
主成分分析を活用して、複雑なデータを解釈しやすくできる
一般に、主成分分析(PCA: Principal Component Analysis)は、複雑なデータの中に潜んでいる"本質"を見える化する目的で使われます。
ここで複雑なデータとは「多くの項目で特徴づけられたものの集まり」です。例えば、以下のようなものです。
- エンジンの性能、乗れる人数、排気量、色などの項目で特徴づけられた車100台
- 身長、体重、肌の色、目の色などの項目で特徴づけられた人間100人
- 数学、英語、国語などの試験の点数で特徴づけられた生徒100人
このようなデータを解釈(例えば、グループ分け)するのは大変です。例えば、3つ目の例で考えると、100人の生徒が、三教科とも同じ点数をとれば、みんな同じグループになるだろうと簡単に予測できますが、そのような状況は考えられません。
そこで、主成分分析を使って、自動的に、数学的に、グループ分けすることが効果的です。
主成分分析の基本は、データの散らばりを大きくするような係数を見つけること
以前の記事で、「高次元データを低次元データで表現するための次元圧縮」について述べました。
主成分分析も同じような考え方で理解できます。
例えば、国語の点数を\(x_1\)、算数の点数を\(x_2\)として、以下の式が成り立っているとします。
$$y = w_1x_1 + w_2x_2$$
これは、国語と算数という2次元のデータが、\(y\)という1次元に変換されているとみることができます。
しかし、式中の\(w_1\)と\(w_2\)は、どのように決めたら良いんでしょうか。例えば、\(w_1 = w_2 = 1\)でもいいんでしょうか。
それは良くありません。なぜなら、Aさんが国語60点、算数40点で、Bさんが国語35点、算数65点のような場合、どちらも\(y = 100\)となり区別できないからです(図でみると、影を区別できないことに対応します)。
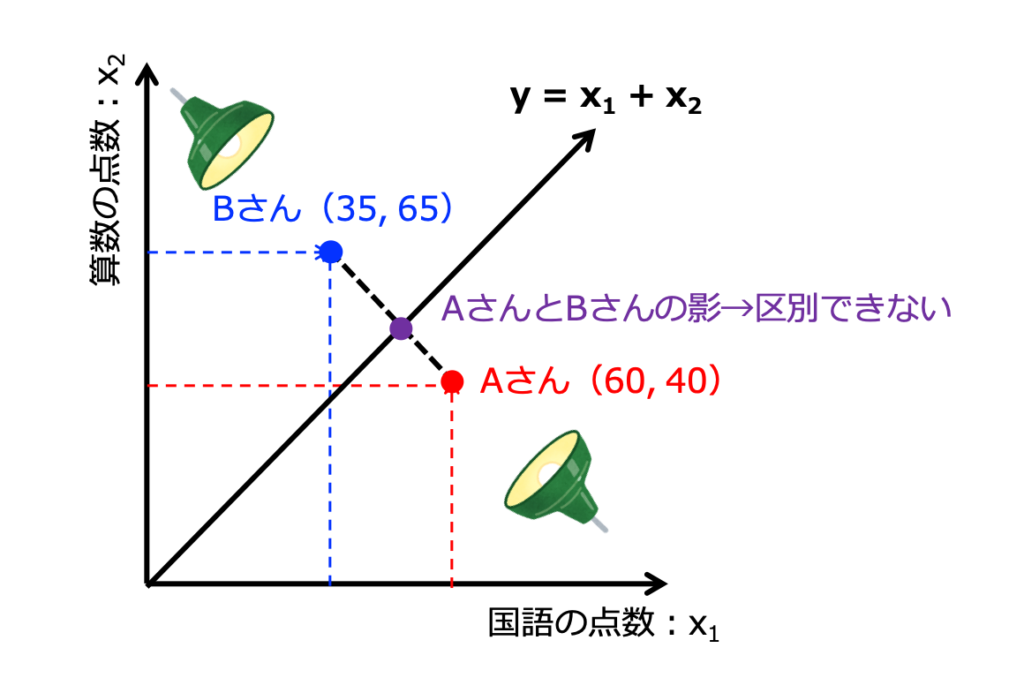
したがって、主成分分析の目的は、影をうつした時にデータの散らばり具合が大きくなるように、\(y\)の式中の\(w\)の値を決定することになります。
専門用語では、射影したデータの分散を最大にする係数ベクトルを決定する、また、標本分散共分散行列の最大固有値に対応する固有ベクトルを決定することが目的になります。
また、影をうつした時にデータの散らばり具合がもっとも大きくなる軸を「第一主成分」、次に大きくなる軸を「第二主成分」と呼びます。
※主成分分析は、因子分析とは違います。因子分析は、観測データという結果に影響した因子を探るアプローチで、主成分分析は、観測データから主成分を合成するアプローチです。
主成分分析はさまざまなプログラミング言語で実行可能(Pythonを例に解説)
主成分分析は、RやRuby、Excel(エクセル)など、さまざまな言語やソフトウェアを使って実行することができます。
ここでは、Pythonを使って主成分分析を行う流れについて紹介します。
まず、Pythonを使用したデータ解析においては必須とも言えるライブラリをインストールします。
$ pip install numpy
$ pip install scipy
$ pip install pandas加えて、機械学習のライブラリである"scikit-learn"も同様にインストールします。
$ pip install scikit-learnそれでは、Pythonを立ち上げます。
$ python今回は、以前の記事でも使用したように、アヤメの観測データ(花弁の長さ、花弁の幅、ガクの長さ、ガクの幅)を使用したいので、以下のコードを実行します。アヤメの観測データは、"scikit-learn"の"datasets"の中で提供されています。
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()"iris.data"と記述することにより、観測データ(花弁の長さ、花弁の幅、ガクの長さ、ガクの幅)を取得することができます。
次に、観測データを基準化(標準化)するために以下のコードを実行します(ただし、観測データの測定単位が大きく異なっていなければ、基準化は必要ありません)。
>>> from sklearn.preprocessing import StandardScaler
>>> scaler = StandardScaler()
>>> scaled_data = scaler.fit_transform(iris.data)上のステップで準備したデータ(scaled_data)を使って、主成分分析を行うために、以下のコードを実行します。
>>> from sklearn.decomposition import PCA
>>> pca = PCA()
>>> pca_data = pca.fit_transform(scaled_data)主成分分析は、以上で終わりです。
第一主成分は"pca_data[:, 0]"、第二主成分は"pca_data[:, 1]"に格納されています。また、各主成分に含まれる情報量を測るための基準である「寄与率」に関しては、以下のコードを実行することで得られます。
>>> pca.explained_variance_ratio_参考文献
小西貞則「多変量解析入門 ー線形から非線形へー」岩波書店

