目次(まとめ)
◾️ 注目している確率変数の分布を求める
◾️ 検出力を確保するために必要なサンプル数を求める
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、2013年に行われた統計検定1級の統計応用の医薬生物学分野の問題(問3)を取り上げて、解答を得るための方針について解説します(問題の詳細については、参考文献などをご覧ください)。
この問題では、さまざまな医院の患者に対する2つの処置の効果を検証する比較研究について取り扱っています。
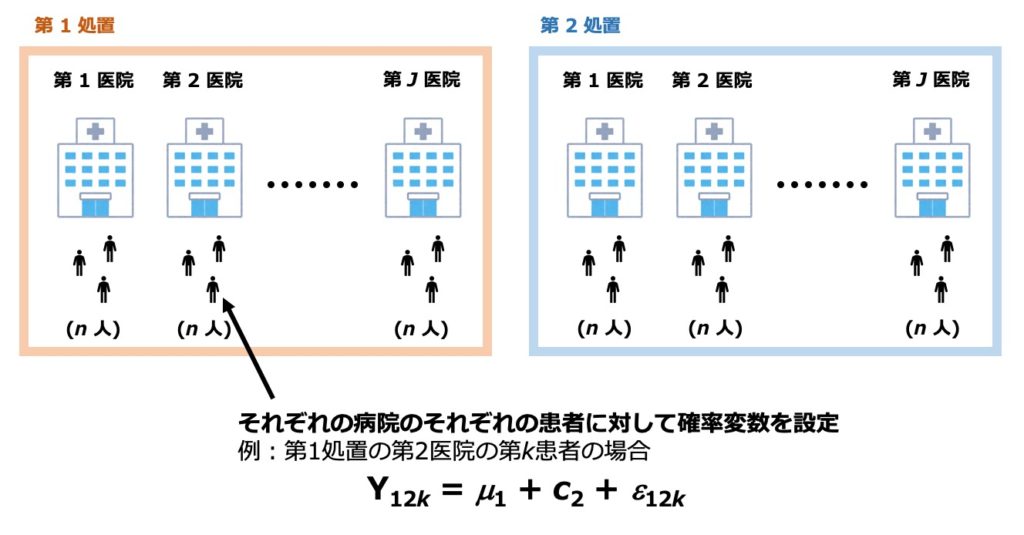
注目している確率変数の分布を求める
第 \(j\) 医院における患者について平均値を考えると、患者数は \(n\) 人なので、以下のようになります。
$$\overline{Y}_{ij} = \frac{Y_{ij1} + Y_{ij2} + ... + Y_{ijn}}{n} = \frac{\sum_{k = 1}^n Y_{ijk}}{n}$$
ここで、
$$Y_{ijk} = \mu_i + c_j + \epsilon_{ijk}$$
であり、\(\mu_i\) が第 \(i\) 処置の効果、\(c_j\) が第 \(j\) 医院の効果、\(\epsilon_{ijk}\) が患者の個体間変動とされています。
また、\(c_j\) は、平均 \(0\)、分散 \(\sigma_c^2\) の正規分布にしたがい、\(\epsilon_{ijk}\) は、平均 \(0\)、分散 \(\sigma_\epsilon^2\) の正規分布にしたがうことがわかっています。
この問題では、第 \(j\) 医院における患者の平均値について、その分布(つまり、平均と分散)を考えています。
まず、平均を考えます。
第 \(j\) 医院には \(n\) 人の患者がいて、当然、全員同じ処置 \(i\) を受けることになります。例えば、第1処置の第2医院の患者 \(n\) 人について、その平均値の平均を考えるイメージです。
この場合、1人目は \(\mu_i + c_j + \epsilon_{ij1}\)、2人目は \(\mu_i + c_j + \epsilon_{ij2}\)、という風に \(n\) 人を考えることになりますが、\(\epsilon_{ijk}\) の平均が \(0\) であることから、結局、今考えている平均は \(\mu_i + c_j\) になります。
同様に、分散を考えると、結局、患者間のばらつきを考えることになり、\(\epsilon_{ijk}\) の分散が \(\sigma_\epsilon^2\) であり、\(n\) 人を考えるので、以下のようになります。
$$V[\overline{Y}_{ij}] = \frac{\sigma_\epsilon^2}{n}$$
さらに、この問題では、第 \(i\) 処置群の患者の平均値について、その分布(つまり、平均と分散)を考えています。
第 \(i\) 処置群の患者は、\(J\) 個の医院に \(n\) 人ずついるので、全体で \(nJ\) 人います。
まず、平均を考えると、第1医院の1人目は \(\mu_i + c_1 + \epsilon_{i11}\)、2人目は \(\mu_i + c_1 + \epsilon_{i12}\)、・・・、第2医院の1人目は \(\mu_i + c_2 + \epsilon_{i21}\)、2人目は \(\mu_i + c_2 + \epsilon_{i22}\) という風になりますが、\(c_j\) の平均が \(0\)、\(\epsilon_{ijk}\) の平均が \(0\) であることから、結局、今考えている平均は \(\mu_i\) になります。
分散は、\(nJ\) 人の患者間のばらつきと、\(J\) 個の医院間のばらつきを考えることになり、以下のようになります。
$$V[\overline{\overline{Y}}_{i}] = \frac{\sigma_c^2}{J} + \frac{\sigma_\epsilon^2}{nJ}$$
検出力を確保するために必要なサンプル数を求める
確率変数 \(X\) の平均値 \(\overline{X}\)が、平均 \(\mu_X\)、分散 \(\frac{\sigma^2}{N}\) の正規分布にしたがい、確率変数 \(Y\) の平均値 \(\overline{Y}\)が、平均 \(\mu_Y\)、分散 \(\frac{\sigma^2}{N}\) の正規分布にしたがうとします。
ここで、有意水準が \(100\alpha\) %の両側検定を考えるとき、検出力が \(100(1 - \beta)\) %になるように必要なサンプル数 \(N\) は以下のように得られます。
$$N = \frac{2\sigma^2 {z(\frac{\alpha}{2}) + z(\beta)}^2}{(\mu_X - \mu_Y)^2}$$
\(z(\alpha)\) は、標準正規分布の上側 \(100\alpha\) %点です。
例えば、有意水準が5%(\(\alpha = 0.05\))の両側検定を考えるとき、検出力が80%(\(\beta = 0.2\))になるように必要なサンプル数 \(N\) は以下のように得られます。
$$N = \frac{2\sigma^2 {z(0.025) + z(0.2)}^2}{(\mu_X - \mu_Y)^2}$$
\(z(0.025)\) は、標準正規分布の上側2.5%点なので、上側確率が0.025になる "1.96"、\(z(0.2)\) は、標準正規分布の上側20%点なので、上側確率が0.2になる "0.84" を代入すると、必要なサンプル数を取得することができます(標準正規分布表の見方は、こちらの記事をご参照ください)。

