目次(まとめ)
◾️ 超幾何分布の確率関数、平均、分散
◾️ 参考文献
◾️ 関連記事
こんにちは、みっちゃんです。
今回の記事では、当たりのボールとハズレのボールが入った壺の中からボールを取り出したときに、当たりのボールの数がしたがう確率分布である「超幾何分布」を紹介します。
超幾何分布の確率関数、平均、分散
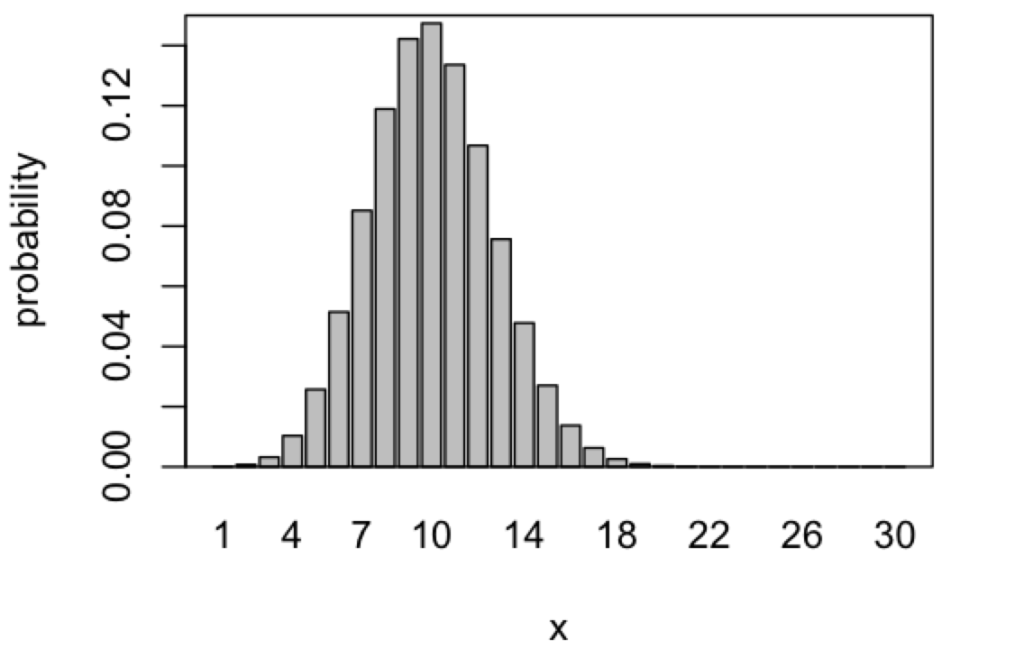
超幾何分布は、上の図で示すような離散分布であり、\(M\) 個の当たりのボールと \(N-M\) 個のハズレのボールが入ってる壺から、\(K\) 個のボールをランダムに非復元抽出したときの、当たりのボールの数 \(X\) についての確率分布です。
したがって、確率分布を決めるパラメータは \(N\)、\(M\)、\(K\) の3つであり、それらを使って確率分布が表現されます。
また、離散分布なので、確率密度関数ではなく、確率関数が定義されます。
確率関数
$$P(X = x | N, M, K) = \frac{\left( \begin{array}{c} M \\ x \end{array} \right)\left( \begin{array}{c} N-M \\ K-x \end{array} \right)}{\left( \begin{array}{c} N \\ K \end{array} \right)} \qquad (x = 0, 1, 2, ..., K)$$
ちなみに、上の図で示している超幾何分布の確率関数は、以下のようにRで実行することで得られます(\(N = 500, M = 50, K = 100\))。パラメータの与え方に注意が必要ですが、 \(M\)、\(N-M\)、\(K\) の順番で与えます。
> x <- 1:30
> barplot(dhyper(x, 50, 450, 100), ylim = c(0, 0.15), names = c(1:30), xlab = "x", ylab = "probability")
> box()
また、超幾何分布の平均(期待値)、分散は、以下のように与えられます。
平均
$$E[X] = K \frac{M}{N}$$
分散
$${\rm Var}(X) = \frac{K(N-K) \frac{M}{N} (1 - \frac{M}{N})}{N-1}$$
参考文献
久保川達也「現代数理統計学の基礎」共立出版

