目次(まとめ)
◾️ 出現確率を考えることで効率的に情報を表現する
◾️ ハフマン符号化では、出現確率を考えて並べた文字列を「葉」に見立てて「木」をつくる
◾️ 平均情報量で考えても同じようなビット数が期待される
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、文字列などの情報をできるだけ少ないビット数で記述するための仕組みである「ハフマン符号化」について解説します。
出現確率を考えることで効率的に情報を表現する
みなさんは、コンピュータを使うときに、どんなボタンを多く使いますか?
例えば、日本語の場合を考えると、「母音」とされる "A", "I", "U", "E", "O" というボタンは押す機会が多いのではないでしょうか?
一方で、使わないボタンには、どんなものがあるでしょうか?
例えば、"Q" や "V" はなかなか使わないボタンかもしれません。
つまり、私たちが文字列をコンピュータ上で書くとき、その1つ1つの文字の出現確率は自ずと違いがでてくることになります。
コンピュータの内部では、すべての情報を "0" か "1" で表現しているため、1つ1つの文字も "0" と "1" の組み合わせで表現することになりますが、例えば、"A" という文字を "00000000"、"Q" という文字を "0000" と表現するとどうなるでしょうか?
出現確率が高い文字に 8ビットを費やし、出現確率が低い文字に4ビットを費やすことになり、非効率であることが明らかです。
そこで「ハフマン符号化」という仕組みが提案されました。
ハフマン符号化では、出現確率を考えて並べた文字列を「葉」に見立てて「木」をつくる
ここでは例として「AQUA」という文字列を、"0" と "1" をできるだけ効率的に組み合わせて表現することを考えます。
それぞれの文字の出現確率を「A: 50%」「Q: 10%」「U: 40%」とします。
「ハフマン符号化」は、以下の手順で行います。
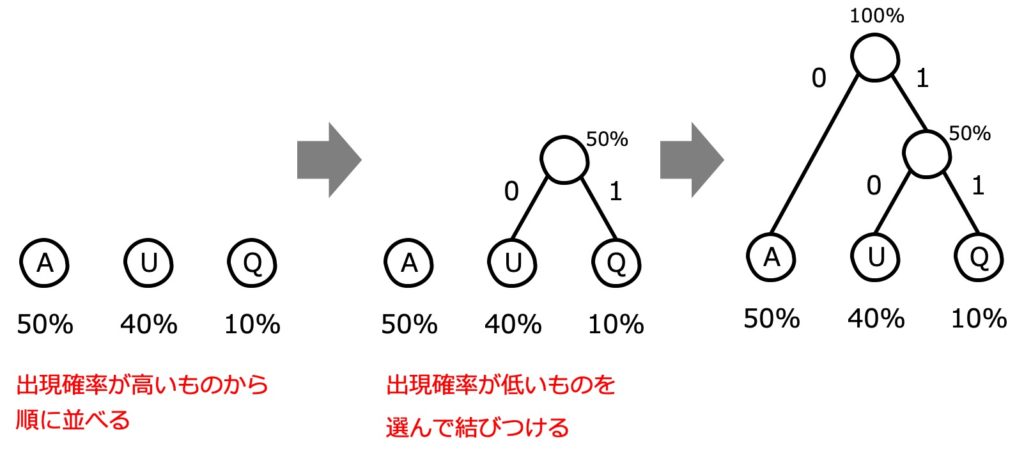
❶ 出現確率が高い文字から順に並べておく
❷ 出現確率が低い文字の「親」に相当する○を描き結びつける(このとき左に "0"、右に "1" と記入します)
❸ ❷の繰り返し
この作業が終われば、一番上の○から線を辿りながら、それぞれの文字を表現するための "0" と "1" の組み合わせを取得できます。
この場合には、「A: 0」「U: 10」「Q: 11」という表現になります。
したがって、「AQUA」という文字列は「0 11 10 0」と表現されるわけです。
また確率の視点から見ると、50%の出現確率のある "A" という文字が1ビット、40%の出現確率のある "U" という文字が2ビット、10%の出現確率のある "Q" という文字が2ビットで表現されるということで、平均1.5ビット(= 0.5*1 + 0.4*2 + 0.1*2 )で文字を表現できているということになります。
平均情報量で考えても同じようなビット数が期待される
以前の記事で「平均情報量」の考え方を紹介しました。
「情報量」は「出現確率」から計算することができ、さらに「平均情報量」は「出現確率」と「情報量」をかけあわせることで計算できることを紹介しました。
ここでも「平均情報量」を計算してみます。
$$(平均情報量) = 0.5*(-{\rm log}_2 (0.5)) + 0.4*(-{\rm log}_2 (0.4)) + 0.1*(-{\rm log}_2 (0.1)) = 1.36$$
よって、答えは1.36ビットとなり、上で計算した1.5ビットに近い値が得られることがわかります。
参考文献
きたみりゅうじ「キタミ式イラストIT塾 応用情報技術者」技術評論社

