目次(まとめ)
◾️ 決定木では、単純な識別規則を組み合わせてデータを識別する
◾️ ランダムフォレストでは、決定木を組み合わせて識別性能を上げる
◾️ 決定木、ランダムフォレストを使った学習と予測をRを使って実行する
◾️ 関連記事(Pythonを使った決定木)
◾️ 参考文献
こんにちは、みっちゃんです。
今回の記事では、「決定木によるグループ分けの性能を向上させたい」という方向けに、決定木を組み合わせたランダムフォレストを用いた分類について紹介します。
決定木では、単純な識別規則を組み合わせてデータを識別する
決定木とは、単純な識別規則を組み合わせて複雑な識別を可能にし、データを識別する(決定木についてよく知らない方はこちらもご参照ください)。
以前の記事では、決定木を作るための入力データ(学習データ)として、150人の生徒の4教科のテストの点数によってグループ分けされたデータを想定して、以下のような学習データを準備しました。
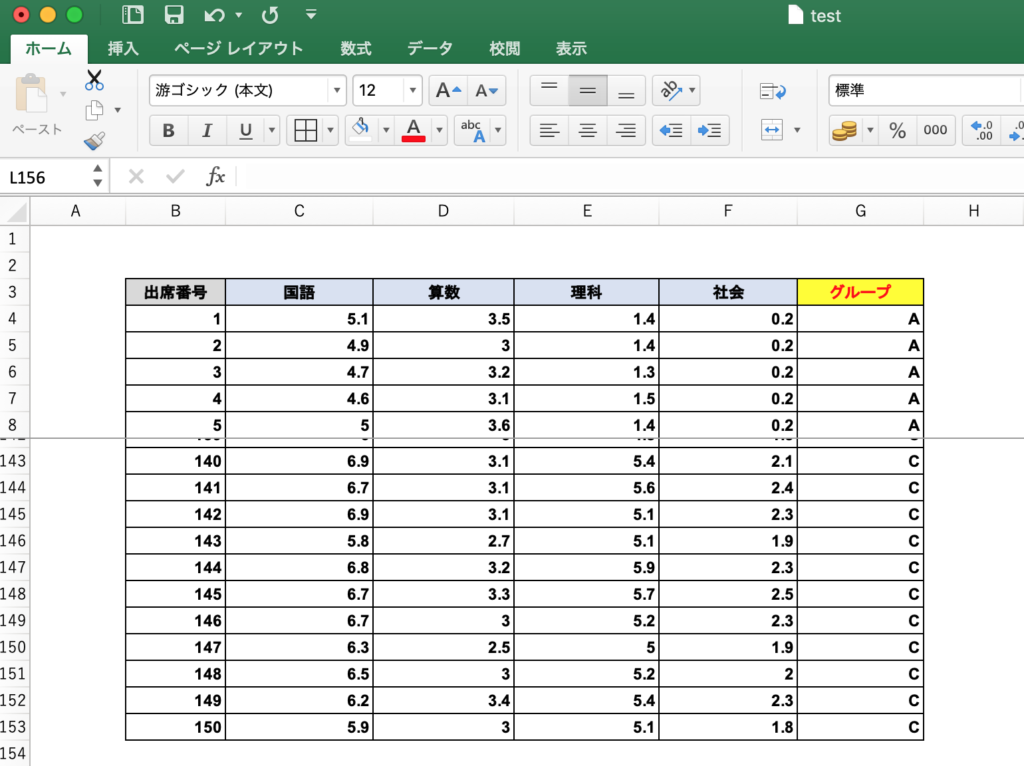
このデータをもとに、以下のような決定木を作ることができます(決定木の見方はこちら)。
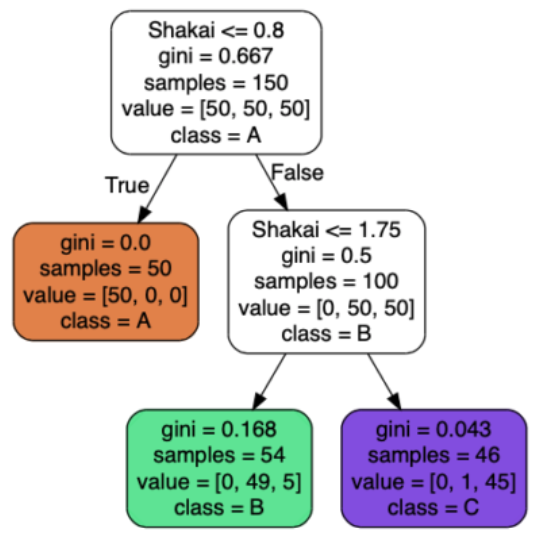
このように「True (Yes)」か「False (No)」を選択していくだけで、学習データのグループ分けが可能な決定木ですが、欠点があります。
決定木の欠点は、学習データが少し変わると、グループ分けの性能が大きく変わってしまうという点です。
そこで、複数の学習データを準備して、それぞれの学習データで決定木を組み合わせて、全ての決定木から得られた結果の「多数決」で新しいデータのグループ分けを行うための手法が提案されています。
ランダムフォレストでは、決定木を組み合わせて識別性能を上げる
ランダムフォレストは、複数の学習データから構築した複数の決定木を用いて、多数決により新たなデータのグループを決定する手法の1つです。
特にランダムフォレストでは、それぞれの決定木を構築する際に用いる学習データの中から、分岐点ごとにランダムに特徴を選択することにより、決定木間のばらつきを大きく、つまり、多様な決定木を作り出す工夫がされています。
決定木、ランダムフォレストを使った学習と予測をRを使って実行する
ここでは、説明のために、Rにあらかじめ準備されているアヤメのデータ(iris)を使用します。
便宜上、以下のように、"data" という変数に "iris" のデータを保存します。
> data <- iris
> head(data)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
> dim(data)
[1] 150 5"data" は、全体で150行ありますが、そのうち8割に相当する120行のデータを学習データ(決定木を作るためのデータ; training_data)、残り2割に相当する30行のデータをテストデータ(決定木の分類性能を評価するためのデータ; test_data)にするために、以下のような操作を行います。
> ind <- sample(nrow(data), nrow(data)*0.8)
> ind
[1] 109 9 18 85 51 76 130 110 41 94 116 37 10 74 61 106 87 49
[19] 5 33 145 25 78 80 112 95 113 115 73 52 11 20 146 13 88 3
[37] 148 57 82 39 15 58 69 98 150 99 12 63 75 79 111 117 17 89
[55] 23 119 147 36 83 29 44 1 144 123 64 24 124 14 84 132 53 59
[73] 137 135 42 22 140 67 66 50 122 104 118 55 62 48 60 141 133 46
[91] 128 136 105 28 43 143 108 31 19 101 2 56 8 81 103 102 26 21
[109] 27 47 96 120 77 38 16 125 32 6 86 72
> train_data <- data[ind,]
> test_data <- data[-ind,]同じような操作は、以下のようにしても実行できます。
> ind <- sample(c(TRUE, FALSE), nrow(data), replace=TRUE, prob=c(0.8, 0.2))
> ind
[1] TRUE TRUE TRUE TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
:
[145] TRUE FALSE TRUE TRUE TRUE FALSE
> train_data <- data[ind,]
> test_data <- data[!ind,]"sample" 関数は、ランダムに "nrow(data)" 個の "TRUE" または "FALSE" を生成します。したがって、実行するたびに、違う結果が得られます。
また、"prob=c(0.8, 0.2)" とすることで "TRUE" の割合が約8割になるようになっています。
※この場合、厳密に、8割:2割にデータが分けられないので注意してください。
決定木
まず決定木による学習は、Rの "rpart" ライブラリを使って、以下のように実行できます。
# > install.packages(rpart) #必要の場合のみ
> library(rpart)
> tree <- rpart(Species~., train_data)
> tree
n= 120
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 120 77 virginica (0.34166667 0.30000000 0.35833333)
2) Petal.Length< 2.7 41 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.7 79 36 virginica (0.00000000 0.45569620 0.54430380)
6) Petal.Width< 1.75 40 5 versicolor (0.00000000 0.87500000 0.12500000) *
7) Petal.Width>=1.75 39 1 virginica (0.00000000 0.02564103 0.97435897) *"rpart" 関数では、目的変数を "Species"、説明変数を "." で示しています。ここで、"." とは、目的変数以外の全ての変数です。
得られた決定木を用いて、テストデータを正しく分類(予測)できるか、以下のようにテストします。
> predicted_tree <- predict(tree, test_data, type="class")"type" には、"class"、"prob"、"vector"、"matrix" から選択できます。"class" を選択する場合には、"test_data" に対して予測されたグループが表示されます。また、"prob" を選択する(もしくは、何も選択しない)と、なぜそのグループに予測されたのかという情報が得られます。
以下のように、予測されたグループと、本来のグループがどれぐらい正しいのか確認することができます。
> table(predicted_tree, test_data[,5])
predicted_tree setosa versicolor virginica
setosa 9 0 0
versicolor 0 14 0
virginica 0 0 7ランダムフォレスト
ランダムフォレストによる学習は、Rの "randomForest" ライブラリを使って、以下のように実行できます。
# > install.packages(randomForest) #必要の場合のみ
> library(randomForest)
> forest <- randomForest(Species~., train_data)
> forest
Call:
randomForest(formula = Species ~ ., data = train_data)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 7.5%
Confusion matrix:
setosa versicolor virginica class.error
setosa 41 0 0 0.0000000
versicolor 0 32 4 0.1111111
virginica 0 5 38 0.1162791出力結果から、このランダムフォレストでは、500個の決定木を組み合わせて、学習していることがわかります。この数は、"ntree = 500" がデフォルトになっているためで、自由に変更することができます。
また、 ランダムに選択された特徴の数は、2個になっていることがわかります。この数は、"mtry = 2" がデフォルトになっているためで、自由に変更することができます。
(例)
> forest <- randomForest(Species~., train_data, ntree = 1000, mtry = 1)得られたランダムフォレストを用いて、テストデータを正しく分類(予測)できるか、以下のようにテストします。
> predicted_forest <- predict(forest, test_data)"predicted_forest" には、"test_data" に対して予測されたグループが保存されています。
以下のように、予測されたグループと、本来のグループがどれぐらい正しいのか確認することができます。
> table(predicted_forest, test_data[,5])
predicted_forest setosa versicolor virginica
setosa 9 0 0
versicolor 0 14 0
virginica 0 0 7
